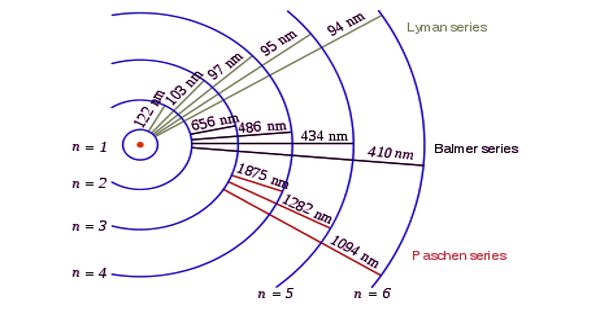
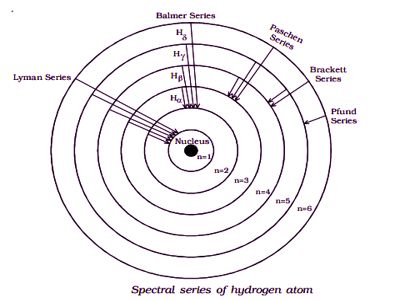
Spectral Series of Hydrogen Atom
Whenever an electron in a hydrogen atom jumps from a higher energy level to the lower energy level, the difference in energies of the two levels is emitted as radiation of a particular wavelength. It is called a spectral line. As the wavelength of the spectral line depends upon the two orbits (energy levels) between which the transition of electron takes place, various spectral lines are obtained. Spectral series is the set of wavelength arranged in a sequential fashion. The different wavelengths constitute spectral series which are the characteristic of the atoms emitting them. The following are the spectral series of a hydrogen atom.
(i) Lyman series
The series was discovered during the years 1906-1914, by Theodore Lyman. When the electron jumps from any of the outer orbits to the first orbit, the spectral lines emitted are in the ultraviolet region of the spectrum and they are said to form a series called Lyman series (Figure). All the wavelength of Lyman series falls in Ultraviolet band.
Here, n1 = 1, n2 = 2,3,4 …
The wavenumber of the Lyman series is given by,
ϋ = R [1 – (1/n22)]
(ii) Balmer series
The series was discovered during the years 1885, by Johann Balmer. When the electron jumps from any of the outer orbits to the second orbit, we get a spectral series called the Balmer series. In astronomy, the presence of Hydrogen is detected using the H-Alpha line of the Balmer series, it is also a part of the solar spectrum. All the lines of this series in hydrogen have their wavelength in the visible region. Here n1 = 2, n2 = 3,4,5 …
The wavenumber of the Balmer series is,
ϋ = R [1/22 – (1/n22)] = R [1/4 – (1/n22)]
The first line in this series (n2 = 3), is called the Hα-line, the second (n2=4), the Hβ-line, and so on.
(iii) Paschen series
The series was first observed during the years 1908, by a German physicist Friedrich Paschen. This series consists of all wavelengths which are emitted when the electron jumps from outermost orbits to the third orbit. Here n2 = 4,5,6 … and n1 = 3. The shortest wavelength of the next series, i.e., the Brackett series overlaps with the Paschen series. From this series, all subsequent series overlap. This series is in the infrared region with the wavenumber given by,
ϋ = R [1/32 – (1/n22)] = R [1/9 – (1/n22)]
(iv) Brackett series
The series was first observed during the years 1922, by an American physicist Friedrich Sumner Brackett. The series obtained by the transition of the electron from n2 = 5, 6… to n1 = 4 is called the Brackett series. The wavelengths of these lines are in the infrared region. All the wavelength of Brackett series falls in the Infrared region of the electromagnetic spectrum. The wavenumber is,
ϋ = R [1/42 – (1/n22)] = R [1/16 – (1/n22)]
(v) Pfund series
The series was first observed during the years 1924, by August Harman Pfund. The lines of the series are obtained when the electron jumps from any state n2 = 6, 7… to n1=5. This series also lies in the infrared region. All the wavelength of Pfund series falls in the Infrared region of the electromagnetic spectrum.
The wave number is,
ϋ = R [1/52 – (1/n22)] = R [1/25 – (1/n22)]