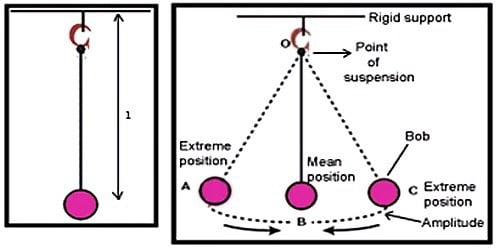
A simple pendulum has a small-diameter bob and a string that has a very small mass but is strong adequate not to stretch significantly.
The period of a simple pendulum is given by T = 2π √l/g
Where, l = Length of a simple pendulum; g = acceleration due to gravity.
From the equation, we can write the relation between the time period of a pendulum and acceleration due to gravity as T is inversely proportional to √g. This relation is referred to as the fourth law of the simple pendulum. In ideal theory, the suspending material will have no mass but in realism that is not feasible.
- 1st law or the law of isochronism:
The time period of the simple pendulum is independent of the amplitude, provided the amplitude is sufficiently small. This property is known as the law of isochronism. The time period (T) is constant when effective length (L) and gravity (g) are constants. This means that a pendulum will take same time in completing each oscillation, whatever is the amplitude, provided the latter does not exceed 4o. So the time period of oscillation of a simple pendulum is independent of the amplitude of vibration, provided its amplitude does not exceed 4o. The oscillation of the simple pendulum is isochronous.
- 2nd law or the law of length:
The time period of the simple pendulum is directly proportional to the square root of its length. This property is known as the law of length. When acceleration due to gravity (g) is constant, the time period (T) of oscillation of a simple pendulum is directly proportional to the square root of its effective length (L). The period of oscillation of a simple pendulum of constant length is independent of its amplitude, provided the amplitude is small.
So, T ∞ √L, when g is constant.
- 3rd law or the law of acceleration:
The time period of a simple pendulum is inversely proportional to the square root of the acceleration due to gravity at that place. This property is known as the law of acceleration due to gravity. When effective length (L) is constant, the time period (T) of oscillation of a simple pendulum is inversely proportional to the square root of the acceleration due to gravity (g) at a place of observation.
So, T ∞ √1/g, when L is constant.
- 4th law or the law of mass:
The time period of oscillation of a pendulum at a place independent of mass and material of the bob provided the effective length of the pendulum is constant. As the expression doesn’t contain the term ‘m’, the time period of the simple pendulum is independent of the mass and material of the bob. This property is known as the law of mass.
Uses of Simple Pendulum
Since the time period of a simple pendulum depends on the length and acceleration due to gravity at a given place, it is used to determine the time in clocks that work on the standard of the simple pendulum. It is also used to find out the acceleration due to gravity at a place.