Representation of Vector by Unit Vector or with Components

Representation of vector by unit vector or with components

When a vector is represented graphically, its magnitude is represented by the length of an arrow and its direction is represented by the direction of the arrow. While expressing a vector with components we will consider two cases. e.g. in two dimensions and in three dimensions. Here two dimensional case is discussed below.

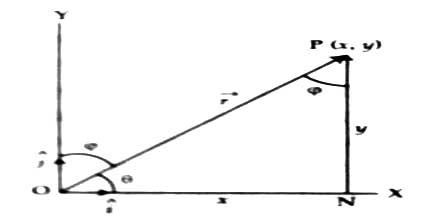
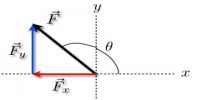
Resolution in two dimensions: Let OX and OY be the straight lines perpendicular to each other and represent X and Y axes respectively [Figure].

In XY plane the line OP, making an angle θ with X-axis, represents the vector ř both in magnitude and direction. Let consider the co-ordinate of P is (x, y) and in positive X and Y-axes corresponding unit vectors are ȋ and ĵ respectively.

Let the normal PN be drawn from P on X-axis.

Now from figure, we get

ON = x; NP = y and OP = r

so, ON^→ =  xȋ, NP^→ = yĵ ; and OP^→ = ř

From the triangle rule,

OP^→ = ON^→ + NP^→

or, ř = ȋ + ĵ

Modulus of this vector,

From figure, we get;

OP² = ON² + NP²

or, r² = i² + y²

then, r = √( i² + y²)