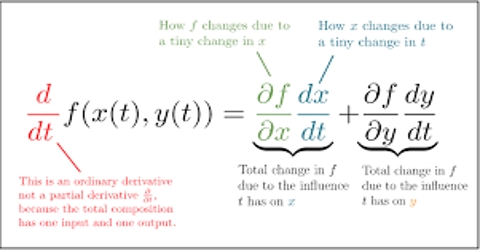General rule for differentiation of a scalar quantity is as follows:
A scalar quantity is a one dimensional measurement of a quantity, like a temperature, or weight. It changes with the change in their magnitude. Ordinary rules of algebra are followed by scalar quantities to perform operations like addition, subtraction and multiplication
(a) Firstly, the co-efficient of the variable quantity is to be multiplied by the power.
(b) Then ‘1’ is to be subtracted from the power of the variable quantity.
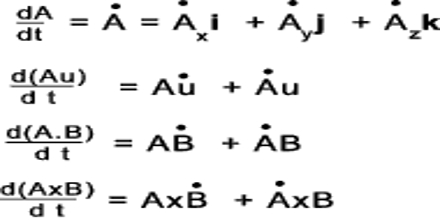
Example: Let the distance, s = 16 t2. Here 16 is the co-efficient, t is the variable quantity and 2 is the power. According to the above rule, firstly 16 is to be multiplied by power 2 which gives 32. And subtraction of 1 from the power 2 of the variable quantity gives 1.
so, ds/dt = v = 32t
Practical Example:
Time – Scalar quantities refer to time; the measurement of years, months, weeks, days, hours, minutes, seconds etc.
Volume – Scalar quantity can refer to the volume of the medium.