Angular momentum
The vector product of the radius vector and the linear momentum of a revolving particle is called angular momentum.
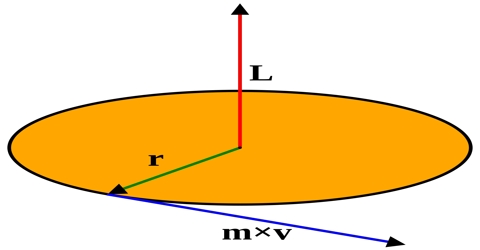
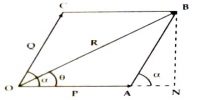
Explanation: Suppose ř = radius vector of a particle rotating with respect to its centre of rotation and Ƥ = linear momentum of the body. Hence, according to the definition the angular momentum Ĺ = ř x Ƥ
It is a vector quantity.
Direction and magnitude: The magnitude of angular momentum is: L = rP sin θ
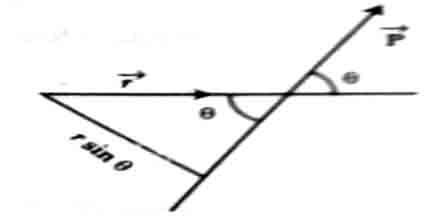
Here θ is the angle between ř and Ƥ (Figure). The perpendicular distance of the line of action of the momentum from the centre of rotation is: r sin θ. So, the product of linear momentum of any particle and the perpendicular distance or the line of action of the momentum from the centre of rotation gives the magnitude at the angular momentum.
The direction of Ĺ will be perpendicular to the plane in which ř and Ƥ are located. The direction Ĺ will be determined by cross product.
The direction is given by the right hand rule which would give L the direction out of the diagram. For an orbit, angular momentum is conserved, and this leads to one of Kepler’s laws. For a circular orbit, L becomes: L = mvr