Combustors, which are critical components of gas engines and are the chambers in which the combustion that powers the engine takes place, are prone to failure due to fatal high-frequency oscillations during the combustion process. Researchers have discovered what causes them to use advanced time-series analyses based on complex systems, opening up new avenues for solving the problem.
Contained combustion systems, which are essentially combustion chambers, are found in rocket engines. Nonlinear interactions between turbulent fuel and oxidizer flow, sound waves, and heat produced by chemical reactions cause an unstable phenomenon known as ‘combustion oscillations’ in these chambers. The force of these oscillations on the body of the combustion chamber – the mechanical stress on the chamber – is great enough to threaten the engine’s catastrophic failure. What is the source of these oscillations? The solution has yet to be discovered.
In a breakthrough published in Physics of Fluids, a team led by Prof. Hiroshi Gotoda, Ms. Satomi Shima, and Mr. Kosuke Nakamura from Tokyo University of Science (TUS), in collaboration with Dr. Shingo Matsuyama and Dr. Yuya Ohmichi from the Japan Aerospace Exploration Agency (JAXA), used advanced time-series analyses based on complex systems to find out.
A vital piece of gas engines, combustors – the chambers in which the combustion powering the engine occurs — have the problem of breaking down due to fatal high-frequency oscillations during the combustion process.
Prof. Gotoda explains their work, “Our main goal was to reveal the physical mechanism behind the formation and maintenance of high-frequency combustion oscillations in a cylindrical combustor using sophisticated analytical methods inspired by symbolic dynamics and complex networks.” The American Society of Physics covered these findings in their news section, as did the Institute of Physics on their news platform Physics World.
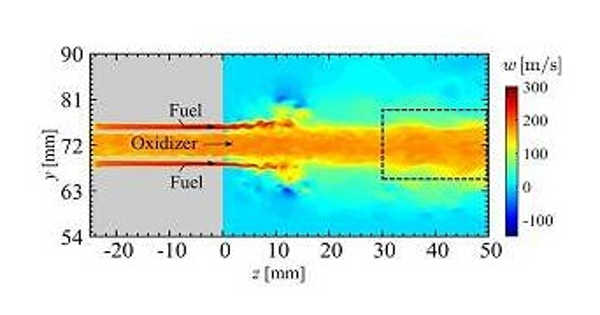
The scientists chose a model rocket engine as the combustor to simulate. They were able to pinpoint and visualize the transition from the stable combustion state to combustion oscillations. They discovered that significant periodic flow velocity fluctuations in fuel injectors affect the ignition process, causing changes in heat release rate. The fluctuations in the heat release rate synchronize with the fluctuations in the pressure inside the combustor, and the cycle continues in a series of feedback loops that sustain combustion oscillations.

A rocket engine forms a high-speed propulsive jet of fluid, usually high-temperature gas, using stored rocket propellants as the reaction mass. Rocket engines are reaction engines that generate thrust by ejecting mass rearward, as stated by Newton’s third law. The majority of rocket engines generate energy through the combustion of reactive chemicals, but non-combusting forms such as cold gas thrusters and nuclear thermal rockets are also available. Rockets are vehicles that are propelled by rocket engines. Rocket vehicles, unlike most combustion engines, carry their own oxidizer, allowing rocket engines to be used in a vacuum to propel spacecraft and ballistic missiles.
Heat is produced during the combustion process as the fuel and oxidizer are converted into exhaust products. Surprisingly, some source of heat is usually required to start combustion. Although gasoline and air are present in your car’s fuel tank, combustion does not occur because there is no heat source. Because heat is both required to start combustion and is a byproduct of combustion, we can see why combustion occurs so quickly. Furthermore, once combustion begins, we do not need to provide a heat source because the heat of combustion will keep things going. We don’t have to keep lighting the campfire; it simply burns.
Furthermore, by examining a spatial network of pressure and heat release rate fluctuations, the researchers discovered that clusters of acoustic power sources form and collapse on a regular basis in the shear layer of the combustor near the injection pipe’s rim, contributing to the combustion oscillations.
These findings, while specific to liquid rocket engines, provide reasonable explanations for why combustion oscillations occur. Prof. Gotoda elaborates, “Combustion oscillations can be fatal to combustors in rocket engines, aero engines, and gas turbines used to generate electricity. As a result, understanding the mechanism of combustion oscillation formation is an important research topic. Our findings will help us better understand the mechanism of combustion oscillations in liquid rocket engines.”
Indeed, these findings are significant, and they can be expected to open up new avenues of investigation for preventing combustion oscillations in critical engines.