Differentiation of a Vector
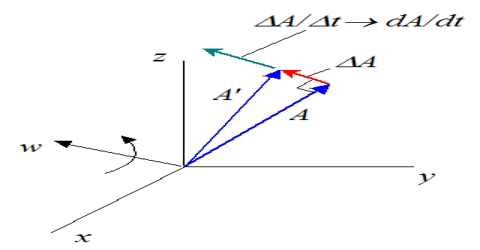
Let V→ (u) be a vector that depends on unit scalar operator u. In mathematical language V is a function of u. Then we can write,
∆R→/∆u = [∆R(u+∆u) – R (u)] / ∆u
here ∆u, means a small increases of u.
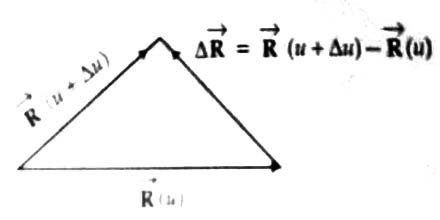
∆R→/∆u is the rate of change of R→ with respect to u. When ∆u tends to zero,
lim∆u→0 ∆R→/∆u = lim∆u→0 [∆R(u+∆u) – R (u)] / ∆u
lim∆u→0 ∆R→/∆u can be written as dR→/du.
So, lim∆u→0 ∆R→/∆u = dR→/du = lim∆u→0 = [∆R(u+∆u) – R (u)] / ∆u
dR→/du; means the rate of change of R→ with respect to u for exceedingly small change of u.
dR→/du; called the differential coefficient of R→ with respect to u.
Process of determining dR→/du is called differentiation.