Determination of work by variable force using integral calculus:
Suppose, a variable force is acting along x-axis on a body. Magnitude of the force depends on distance travelled by the body i.e., F is the function of distance x. In the figure a graph has been plotted showing the variation of F(x) for different values of x.
Total displacement consists of equally divided n number of exceedingly small displacement ∆x, where ∆x is the displacement between x1 and x1 + ∆x. For this small change of displacement the magnitude of force is considered constant and the value of force is F1. So work done by this force tin this small segment is,
∆W1 = F1 ∆x
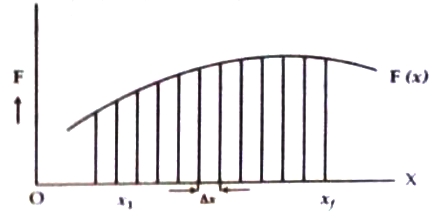
Similarly, second segment is extended between x1 + ∆x to x1 + 2∆x and the small displacement is ∆x. For this small segment constant force is F2. So work done by the force in the second segment is ∆W2 = F2 ∆x. So, total work done by the force F(x) to move the body from position xi to xf is given by,
W = ∆W1 + ∆W2 + ∆W3 + … … …+ ∆WN
= F1∆x + F2∆x + F3∆x + … … … + FN∆x
= N∑K=1 FK ∆x … … … (1)
When ∆x becomes smaller and smaller, that means the value of N becomes very large, calculated value of work done will be more correct. We can get correct value of work done by the force F(x) it ∆x approaches zero and N becomes infinity. Then correct value will be,
W = lim∆x→0 N∑K=1 FK ∆x … … … (2)
But in the language of calculus, the quantity, lim∆x→0 N∑K=1 FK ∆x; is written as:
xf∫xi F(x) dx; which indicates the integration between xi and xf.
So, equation (2) becomes,
W = xf∫xi F(x) dx
Numerically this quantity is the area subtended by the curved line of force and the displacement between x1 and xf. So, by integration work and area can be determined.