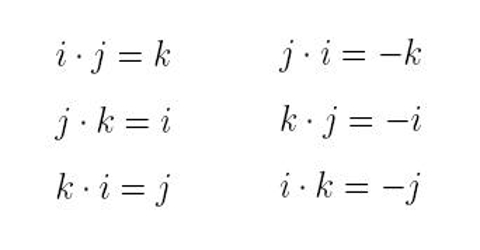Multiplication of unit vectors
Multiplication of a vector by a scalar changes the magnitude of the vector, but leaves its direction unchanged. Geometrically, the dot product of two vectors is the magnitude of one times the projection of the second onto the first.
Let consider three mutually perpendicular axes. These are X, Y and Z. Suppose î, ĵ and ƙ are unit vectors along those three axes.
Let us find their scalar product.
(i) î.î = |î|.|î| Cos 00; as angle between two unit vectors = 00.
= 1 x 1 x 1 = 1
similarly, ĵ.ĵ = 1 and ƙ.ƙ = 1
so, î.î = ĵ.ĵ = ƙ.ƙ = 1
(ii) î.ĵ = |î| |ĵ| cos 900 (angle between X and Y is 900)
= 1 x 1 x 0 = 0
Similarly,
ĵ.ƙ = 0 and ƙ.î = 0
then, î.ĵ = ĵ.ƙ = ƙ.î = 0
Mathematical Example:
Find the scalar product of the two vectors A→ = 9 î + ĵ – 6 ƙ and B→ = 4 î – 6 ĵ + 5 ƙ mid also show that they are perpendicular to each other.
We know, if A→ . B→ = 0 then the vector quantities will be perpendicular to each other.
According to question, it is required that A→ . B→ = AB cos θ = 0
A→ . B→ = AxBx + AyBy + AzBz
so, A→ . B→ = 9×4 + (1x-6) + (-6×5)
= 36 – 6 – 30 = 0
As, A→ . B→ = 0; but, A ≠ 0 and B ≠ 0
so, cos θ = 0 = cos 900
S, the vectors are perpendicular to each other.