Resolution of Vector in Three Dimensional Co-ordinates

Resolution of Vector in Three Dimensional Co-ordinates

While expressing a vector quantity with its components we will consider resolution only in three-dimensional rectangular coordinates.

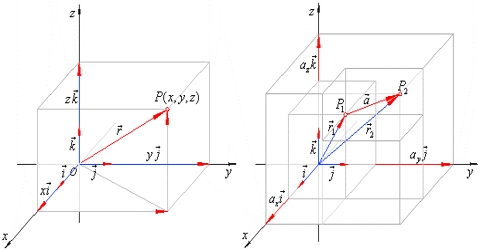
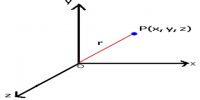
In three dimensional coordinate system, a position vector can be expressed in the following way.

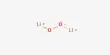
ř = î x + ĵ y + ƙ z. Here position coordinate of P is (x, y, z).

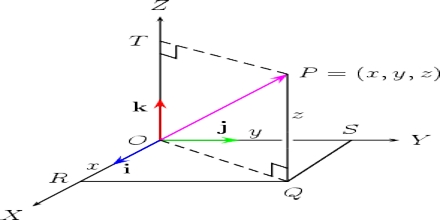
Proof: Let OX, OY and OZ be three lines perpendicular to one another and corresponds to X, Y and Z axes respectively [Figure].

Let a position vector ř be represented by line OP, in this axes-system, both in magnitude and direction.

Let consider that the co-ordinate of P is (x, y, z) and î, ĵ and ƙ are the unit vectors along the axes X, Y and Z respectively. Here PR is drawn normal to plane XY and RQ is normal to OX [Figure].

Now, from figure,

OP = OR + RP and

OR = OQ + QR

so, OP = OQ + QR + RP

but, OQ = x î . QR = y ĵ . RP = z ƙ

and, OP = ř

So, ř = x î + y ĵ + z ƙ

Here, x, y and z are the components of vector ř along X, Y and Z axis respectively.

Modulus of ř:

From figure we get,

OP² = OR² + RP² and, OR² = OQ² + QR²

so, OP² = OQ² + QR² + RP²

or, r² = x² + y² + z²

then, r = √( x² + y² + z²)