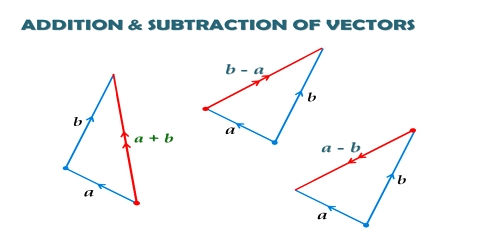
Triangle Law in Geometrical Addition of Vector Quantities
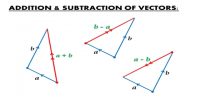
If two similar vectors acting at a point can be represented by two consecutive sides of a triangle taken in order, then the third side will give the resultant vector in the reverse order.
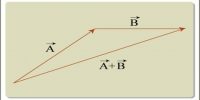
Explanation: We consider two similar vectors, P and Q [Fig]. We like to find the resultant of these vectors by triangle law. We draw AB = P. From the head of B we draw BC = Q which is parallel to Q [Fig].
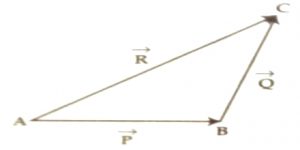
Now, joining the initial point of P and the terminal or end point of Q, let us complete the triangle ABC. The side AC will represent the resultant vector R of P and Q both in magnitude and direction. That means,
AB + BC = AC or, P + Q = R
Again, AB + BC = AC = – CA
or, AB + BC + CA = 0
Conclusion: If three vectors acting simultaneously at a point are represented by three sides of a triangle taken in order, then the result will be zero.