Accurate digit in the experimental result
Accuracy of a measured quantity depends on the accuracy of the associated quantities related to the measured quantity. But when we use calculator for calculation, we get many digits. It is useless to note all these digits after the decimal in the result. The significant digit that is to be kept will be decided by the accuracy of the observable quantities. So, unnecessary digits in the experimental results are to be avoided and only the digits which are reliable in measurement are to be noted. For example, while measuring length by a metre scale, it is not possible to measure accurately less than a millimeter by this scale; hence accuracy of the measurement of length is ± 1 aim.
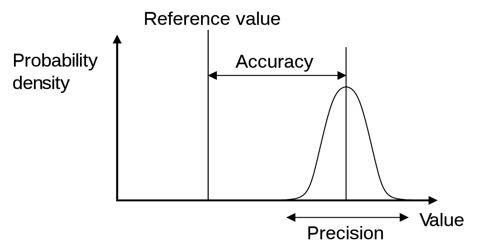
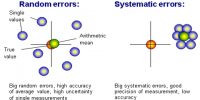
Mean Error: By adopting different precautions we can measure a quantity very nearly its exact value, but never can measure exactly the accurate value. The value that is obtained will have an error within a limit on both sides of the accurate value, which is expressed by ± percentage value.
(1) Mean error or mean deviation: Suppose, only the random error of the measured quantity is being included. If the quantity is measured n times and the values obtained are x1, x2, x3, … … xn, respectively, then the average of the quantities will be,
A = (x1, x2, x3, … … xn)/n
In this measurement only random cam has been included, so the measured value A will be nearer to the actual value of the quantity. In each measurement of the quantity, it may be considered that there is a scull error from the average value A. So, the error that exists in each measurement is respectively,
d1 = x1 – A, d2 = x2 – A, d3 = x3 – A, ……dn = d1 = xn – A
Now, by avoiding the sign of error, if we take the average of these errors we get mean deviation or average error.
Hence, mean deviation or average error, d = (d1 + d2 + d3 + …..+ dn)/n
So, the accurate value of the measured quantity is, x = (A ± d)
(ii) Standard deviation: Sometimes, instead of taking the average of the errors, mean of the squares of the errors are taken and root mean square is found out. This value of root mean square is called standard deviation, D.
So, Standard deviation, D = [√(d12 + d22 + d32 + …..+ dn2)]/n
= (√∑d2)/n
Hence, the actual value of the measured quantity. x = (A ± D). Now, the percentage of error of the measured quantity can be found out in the following way by taking the internationally accepted value of the quantity from the Physical constant table.
Percentage of error of the measured quantity
= [(actual value of the quantity – measured value)/ actual value] x 100%
This is the percentage of error.