Angular displacement
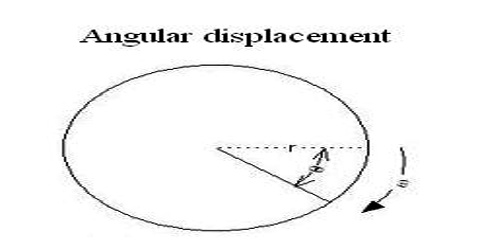
Suppose, on any plane surface like the page of this book, a particle is rotating in circular orbit around a fixed point O. Here axis of rotation will pass through the centre O of the circle and will be perpendicular to the plane of the circle [Fig]. At any moment, in order to know the position of the particle, let consider a stationary straight line OX on that plane. OX is called the reference line.
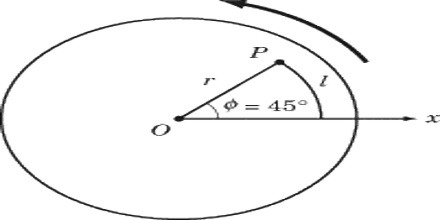
If counting of time is started as soon as the particles crosses the reference line and suppose, after time t the position of the particle is P. Clearly, if the angle θ subtended by the radius vector OP with line OX is known, then the position of the particle will be known completely. The angle θ is called the angular displacement of the particle OP is radius vector.
Definition: The angle through which the radius vector of a particle moves in fixed time interval in a circular motion is called angular displacement of the particle.
Angular displacement is the angle in radians through which a point or line has been rotated in a specified sense about a specified axis. It is the angle of the movement of a body in a circular path. If angular displacement θ is expressed in radian then its relation with the associated arc s is very simple. That is: θ = s/r; here r is the radius vector.