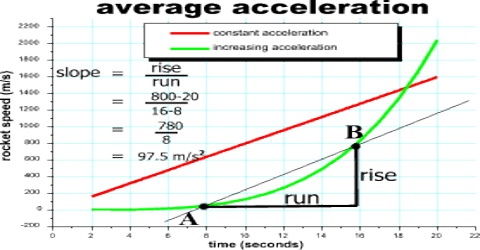
Average acceleration: The average acceleration of an object is its change in velocity divided by the time required for that change. For instance, if the velocity of a marble increases from 0 to 60 cm/s in 3 seconds, its average acceleration would be 20 cm/s/s. This means that the marble’s velocity will increase by 20 cm/s every second.
Explanation: Suppose the velocity of a body at time t0 is v0→ and at later time t the velocity is v→. Here change of time is t – t0 = ∆t and change of velocity is v→ – v0→ = ∆v. So, according to definition the average acceleration of the body.
a→ = (v→ – v0→) / (t – t0) = ∆v/∆t
For one dimensional motion along X-axis, average acceleration will be,
ax→ = ∆vx/∆t î; and its magnitude is,
ax = ∆vx/∆t.

Example: A car accelerates with an initial velocity of 10 m/s for 5s then 20 m/s for 4s finally for 15 m/s for 8s. Calculate the average acceleration?
Solution:
Given: Velocity v1 = 10 m/s, v2 = 20m/s, v3 = 15m/s
Time taken t1 = 5s, t2 = 4s, t3 = 8s
Total velocity Δ v = v1 + v2 + v3 = 10 + 20 + 15 = 45 m/s
Total time taken Δ t = t1 + t2 + t3 = 5 + 4 + 8 = 17 s
The average acceleration is given by a = Δv/Δt = 45/17 = 2.647 ms-2