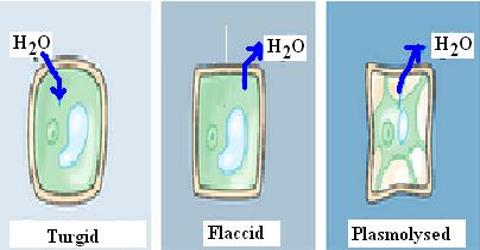
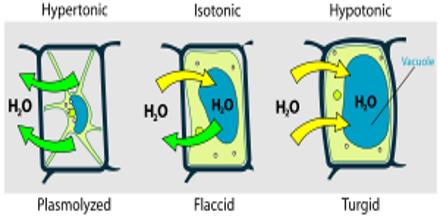
Plasmolysis: Plasmolysis is the process by which cells lose water in a hypertonic solution. Plasmolysis may be defined as the shrinkage of cell protoplasm away from it’s cellulose wall when placed in a hypertonic solution.
During plasmolysis, the cell membrane pulls away from the cell wall. This does not occur in little salt concentration because of the rigid cell wall.
When a plasmolysed cell is placed in a hypotonic solution, the water moves into the cell because of the higher concentration of water outside the cell than in the cell. The cell then swells to become turgid. It is called deplasmolysis.
Types of Plasmolysis
- Concave Plasmolysis: During concave plasmolysis, the protoplasm and the plasma membrane shrink away from the cell wall in places due to the loss of water; the protoplasm is then called protoplast once it has started to detach from the cell wall.
- Convex Plasmolysis: When a cell undergoes complex plasmolysis, the plasma membrane and protoplast lose so much water that they completely detach from the cell wall.