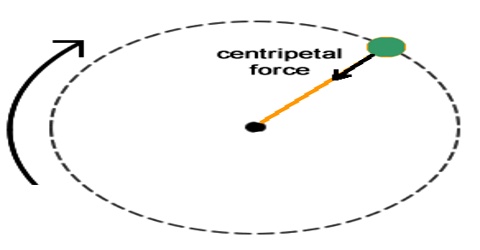
Centripetal force
According to Newton’s first law due to inertia of motion a moving body always intends to move in a straight line with uniform speed. So unless an external force is applied motion of a body does not change automatically. In every moment direction of motion of a rotating body in a circular path changes; so a force always acts on this body from outside.
We have seen before that when a body of mass m rotates in a circular path of radius r with speed v, then a centripetal acceleration v2/r acts on that body. According to Newton’s second law of motion this acceleration is produced due to the action of a force. Clearly, this force will be centripetal as well, i.e., will act along the radius towards the centre and its magnitude will be equal to the product of the mass of the body and the centripetal acceleration i.e., mv2/r. If the action of this tong stops for any reason, then there will not be any force left to rotate the body in the circular path. Then the body will go away along the tangent of the circle and will move with uniform speed in a straight line.
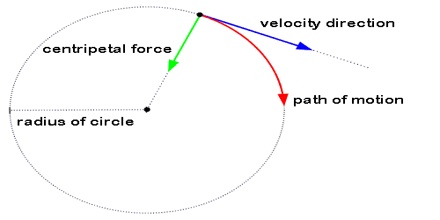
The force for the action of which a body moves in a circular path with uniform Speed and the force which acts perpendicularly to the direction of motion i.e., towards the centre of the circle is called centripetal force.
Centripetal force is a force on an object directed to the center of a circular path that keeps the object on the path. Its value is based on three factors:
1) the velocity of the object as it follows the circular path;
2) the object’s distance from the center of the path; and
3) the mass of the object.
It a body of mass in rotates around a circular path of radius r with uniform speed v, and then the magnitude of the centripetal force is mv2/r. In angular velocity it is expressed as mω2r.