For a single absorbing molecular species in solution, the Beer-Lambert Law states that
A = Ɛ l c
where A is the absorbance, e is the molar absorptivity (extinction coefficient), l is the path length of the cell containing the absorbing solution (usually 1 cm) and c is the concentration of the solution in mol L-1. If a mixture has spectra for each of the individual component compounds of the mixture which has regions where each component dominates the spectrum, then we can use straight forward matrix algebra to determine the concentrations of the mixture components.
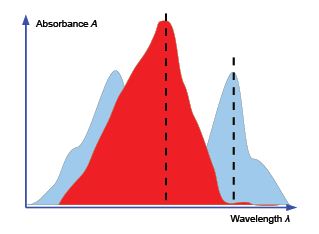
For a solution containing two absorbing species X and Y the overall absorbance measured (Atotal) would the sum of the individual absorbances at wavelengths chosen so that one of the components is the major contributor. For a two component mixture we need two such wavelengths to give two simultaneous equations.
Atotal = Ɛ1 l c1 + Ɛ2 l c2
A student in the teaching lab measured the following absorptivities using a 1 cm path length cuvette for the pure components known to be in the mixture
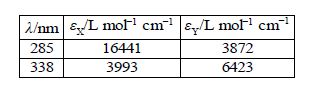
The student was given an unknown mixture of the two compounds X and Y and measured in a 1 cm cuvette the total absorbances of 0.952 at 285 nm and 0.553 at 338 nm. Find the concentrations of X and Y in the mixture by rewriting the data in matrix form for the two simultaneous equations and solving them by the appropriate matrix manipulations.
Solution
For the binary mixture then writing this in matrix form, entering the student’s lab results (without units for clarity), rearranging the matrix equation into the standard simultaneous equations form gives A x = b and solving this by matrix algebra
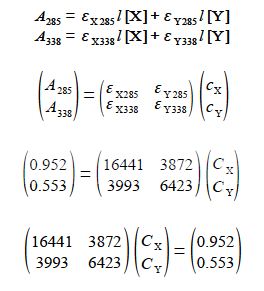

The unknown concentrations from the well-separated spectral regions are to three significant figures
Cx = 4.41x 10-5 molL-1 and cY = 5.87 x 10-1 molL-1
Where there is a substantial overlap of the spectra of the pure components we cannot used matrix algebra methods to solve the simultaneous equations. They are solved by a linear least squares spreadsheet using the Solver algorithm.