From atomic structure we know an electron can only have has an intrinsic spin vector of s = 1/2. From quantum mechanics the magnitude of the spin vector is ׀s׀ is,
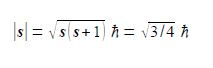
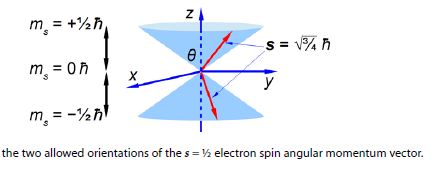
where h (h bar) is Planck’s constant divided by 2π. Quantum mechanics also restricts the value of the component of s along the z-axis of the electron to mZ to ±1/2h (spin up ↑ and spin down ↓). What about the other two Cartesian components of the spin vector (mx and my), can we say anything about them? Due to Heisenberg’s Uncertainty Principle if we know my exactly then we can know nothing about mx and my hence our spin vector points somewhere on a cone of uncertainty as in below Figre. Calculate the half-angle of the cone of uncertainty θ of the electron spin angular momentum vectors.
The 2p electrons have an orbital angular momentum l = lh. From quantum mechanics the magnitude of the orbital angular momentum vector is ׀ l ׀.
׀ l ׀ = √ l (l + 1) h = √2 h
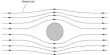
Quantum mechanics also restricts the value of the component along the z-axis to one of three possible values mz equal to -1- lh, 0 h, or – 1h. Again because we know the value of the component along the z-axis exactly, we know nothing about the values along the x-axis and y-axis. The orbital angular momentum vector points somewhere on one of three “cones of uncertainty” as in below Figure. Calculate the half-angles of the cones of uncertainty El of the electron orbital angular momentum vectors.
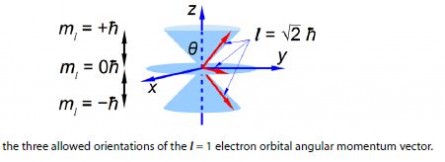
Solution
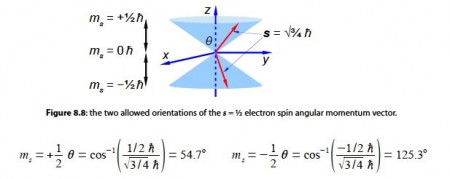
The angles of the two half cones for the electron spin are measured from the positive z direction, so the sn,= -1/2 cone half-angle is 0 = 180°-125.3° = 54.7° from the negative z-axis. The electron orbital angular momentum vector point in one of three orientations for the p atomic orbitals.
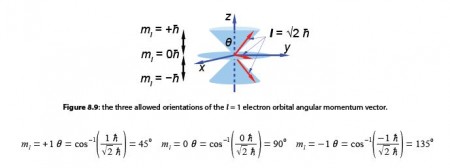
The m1 = -1 cone half-angle is θ = 1800-135° = 45° from the negative z-axis.