=> Write down the Hiickel secular determinant for the acyclic three C-atoms in terms of x, where x = (α – E)/ β.
=> Solve the secular determinant for x and then rewrite the solution in terms of (α – E)/ β and so find the three allowed quantized energies (eigenvalues).
=> Evaluate the normalized wavefunction (eigenvector) for each energy (eigenvalue).
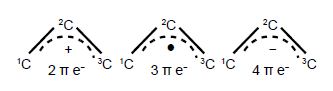
=> Which of the wavefunctions is the HOMO, LUMO or SOMO (singly occupied MO) as appropriate, for each of the allyl cation, radical and anion molecules?
Solution

Since α and β are both have negative values so with increasing energy the eigenvalues are the following
E1 = α + √2 β
E2 = α
E3 = α – √2 β
To find the three eigenvectors (wavefunctions) corresponding to these three eigenvalues we must separately solve the Bickel matrix for ally’ for each energy For E1 = α + √2 β then (α – E1) = – √2 β.
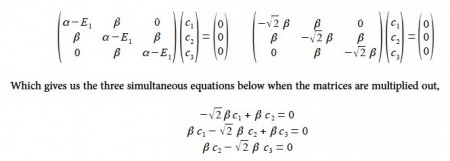
Subtracting the third equation from the first gives c1 = c3. From the first equation c2 = √2 c1, and from the third equation c2 = √2 c3 which when we normalize the coefficients using c12 + c22+ c32 = 1 gives
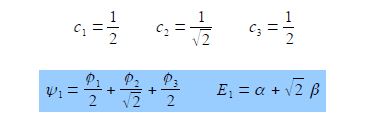
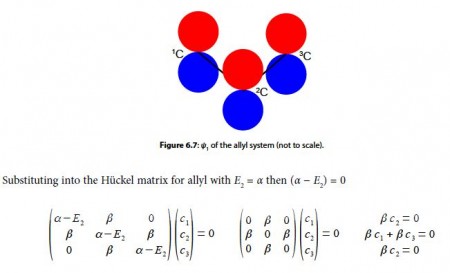
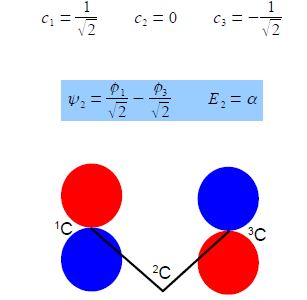
From the first and third simultaneous equations c2 = 0, and from second equation, c1 = – c3 If the coefficients are normalized, then c12 + c22 + c32 = 1 then,
Substituting into the Hiickel matrix for ally) with E3 = α – √2 β then (α – E3) = √2 β
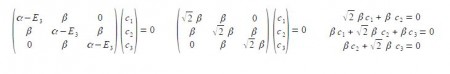
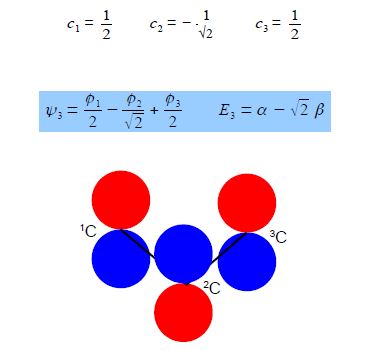
Subtracting the third from the first simultaneous equations c1 = c3 from the first equation c2 = √2 c1; from the third equation c2 = – √2 c3 thus when the coefficients are normalised, then c12 + c22 + c32 = 1 we have,
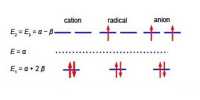
Below Figure shows the MO energy diagrams for the three allyl species.
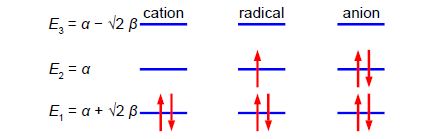
In the allyl cation CH2=CH—CH2+ with 2 π-electrons, then ψ1 is the HOMO and ψ2 is the LUMO. In the allyI radical CH2=CH—CH2+ with 3 π-electrons, then ψ1 has 2 π-electrons and ψ2 is the SUMO with 1 π-electron and ψ3 is the LUMO. In the allyl anion CH2=CH—CH2– with 4 π-electrons, then ψ1 has 2 π -electrons and ψ2 is the HOMO with 2 π-electrons and ψ3 is the LUMO.