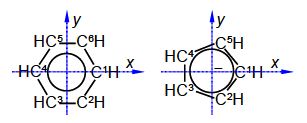
Calculate a set of Cartesian coordinates with respect to the origin for firstly, the carbon atoms only of benzene given that the C-C bond distance is 1.40 A and the benzene ring is a regular hexagon, below Figure. Secondly, the carbon atoms only of the cyclopentadiene anion given that the C-C bond distance is 1.40 A and the five membered ring is a regular pentagon. To tackle this question find the coordinates of C1 and then apply the appropriate symmetry operations to find the coordinates of the remaining carbon atoms, here focus on Molecular Structure Analysis of Cyclic Molecules.
Solution
The C-C distance in benzene is 1.40 A with the angle between neighbouring C-atoms of 360°/6 = 60°. So neighbouring C-atoms form an isosceles triangle with the origin, so half the angle and half the bond distance gives us a right angle triangle with the hypotenuse of (1.40 A/2)/sin(600/2) = 1.40 A. In below Figure the coordinates of C1 are (1.40, 0, 0) after dropping the units for clarity.
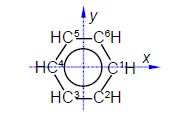
C2 is symmetry related to C1 as a rotation around the z-axis of 300°
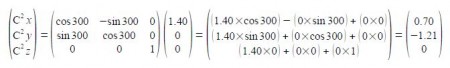
C3 is a reflection in the yz plane of C2 and only changes the x coordinate of C2 to —x
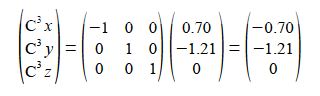
C4 is a reflection in the yz plane of C1 and only changes the x coordinate of C1 to —x
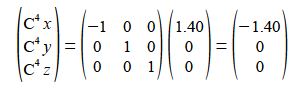
C5 is an inversion through the origin of C2 will change all three coordinates to their negative values
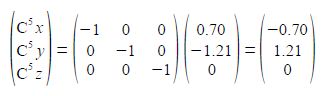
C6 is a reflection in the zx plane of C2 and only changes the y coordinate of C2 to —y
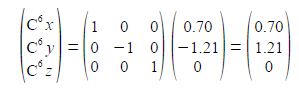
The C-C distance in the cyclopentadiene anion is 1.40 A with the angle between neighbouring C-atoms of 360°/5 = 72°. So neighbouring C-atoms form an isosceles triangle with the origin, so half the angle and half the bond distance gives us a right angle triangle with the hypotenuse of (1.40 A/2)/sin(72o/2) = 1.19 A. So in Fig. 5.19 C1 has the coordinates (1.19, 0, 0) after dropping the units for clarity.
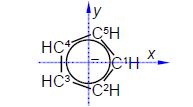


The take home message is that without the use of matrix algebra of symmetry operations these structural problems in Chemistry would involve some complicated non-trivial trig calculations.