Titration of a Strong Acid with a Strong Base
In a strong acid-strong base titration, the acid and base will react to form a neutral solution. At the equivalence point of the reaction, hydronium (H+) and hydroxide (OH-) ions will react to form water, leading to a pH of 7. This is true of all strong acid-strong base titrations.
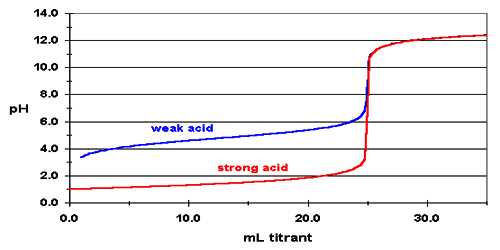
Figure shows a curve for the titration of 25.0 mL of 0.100 mol L-1 HCl solution in the conical flask by 0.100 mol L-1 NaOH solution added from the burette. The pH can be calculated after each addition of base. Sample calculation is shown:
Before any NaOH is added the pH of the solution = – log [H3O+) = – log 0.1 = 1.0. On adding 5.0 mL of NaOH solution the moles of acid left is-
[(25.0 – 5.0) (0.1)] / 1000 = 0.002
Volume of the solution is (25.0 + 5.0) = 30.0 mL.
The concentration of acid left = (0.002 x 1000) / 30.0 mL = 0.067 mol L-1 = [H3O+]
Hence, pH = – log 0.067 = 1.48
Similar calculations can be carried out after addition of each volume of the titre. On addition of 25.0 mL of the base the solution becomes neutral and its pH is 7.0. On adding excess NaOH, say 25.1 ml, the moles of excess;
NaOH = [(25.1- 25.0) (0.1)] / 1000 = 0.01 / 1000 = 1.0 x 10-5 mol L-1.
and, [OH–] = (1.0 x 10-5) (1000) / 50.1
= 0.0002 mol L-1
Hence pOH = – log 0.0002 = 3.70
And pH = 14 – 3.70 = 10.30
Similar calculations for addition up to about 50.0 ml of the base can be done.
Values of pH as calculated when plotted against the volume of NaOH solution added yield a cone like the one shown in Figure.
It can be noted that the pH changes slowly at first until the molar amount of base added is close to the moler amount of HCl, i.e., is until the titration is close to the equivalence point. At the equivalence point the pH is 7.0 as d the acid is completely neutralized by the base and the solution contains only Na+ and Cl– ions.
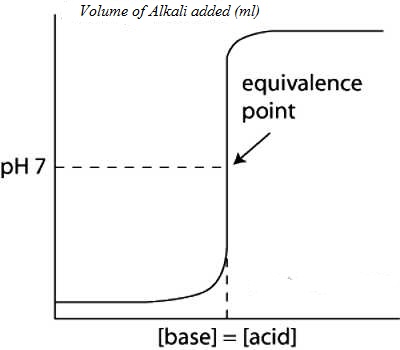
Fig: (Acid based neutralization curve for Strong acid and strong base)
However as the equivalence point is approached the pH changes rapidly and the value rises sharply from about 3 to 10 close to the equivalence point. Beyond this point on the addition of more NaOH the value of pH changes slowly. The volume of NaOH solution where a sharp rise in the pH, occurs is the equivalence point.
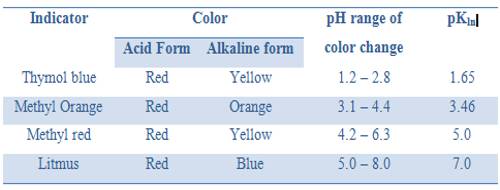
“The equivalence point of a titration may be found with the help of an indicator only if it changes color is the pH range in the vertical portion of the neutralization curve”.
In this case the pH range in the vertical part from 3 to 11. The exact range of pH depends on the concentration of the acid and base.
It was noted that an indicator changes color approximately within a pH = pKln ± 1. So for this titration, an indicator which has pKln lying between 4 and 10 would be suitable. From the table, we can see that methyl orange, methyl red, bromothymol blue or phenolphthalein can be used.