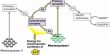
Series resonance or voltage resonance in RLC circuit
The value of current at any instant in a series RLC circuit is given by
I = V/Z
= V / √[R2 + (Xl-XC)2]
= V / √[R2 + (ωL – 1/ωC)]
At a particular value of the angular frequency, the inductive reactance and the capacitive reactance will be equal to each other (i.e.)
ωL = 1/ωC; so that the impedance becomes minimum and it is given by Z = R
i.e. I am in phase with V
The particular frequency νo at which the impedance of the circuit becomes minimum and therefore the current becomes maximum is called Resonant frequency of the circuit. Such a circuit which admits maximum current is called series resonant circuit or acceptor circuit.
Thus the maximum current through the circuit at resonance is
IO = V/R
Maximum current flows through the circuit since the impedance of the circuit is merely equal to the ohmic resistance of the circuit. i.e Z = R
ωL = 1/ωC
ω = 2π v0 = 1/√LC
v0 = 1/2π√LC