A capillary tube of a very fine bore is connected by means of a rubber tube to a burette kept vertically. The capillary tube is kept horizontal as shown in Figure. The burette is filled with water and the pinch – stopper is removed.
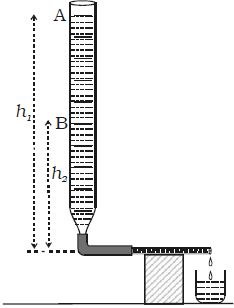
As a fluid flows through a pipe, the layer of water in contact with the tube is acted on by frictional forces slowing it down. The time taken for the water level to fall from A to B is noted. If V is the volume between the two levels A and B, then the volume of liquid flowing per second is V /t. If l and r are the length and radius of the capillary tube respectively, then
V/t = πPr4 / 8η∫ … …. (1)
If ρ is the density of the liquid then the initial pressure difference between the ends of the tube is P1 = h1 ρg and the final pressure difference P2 = h2 ρg. Therefore the average pressure difference during the flow of water is P where
P = (P1 – P2)/2
= [(h1 – h2)/2]*ρg = hρg
Substituting the equation (1) we get,
V/t = πhρgr4 / 8η∫
Or, η = (πhρgr4t) / (8∫V)
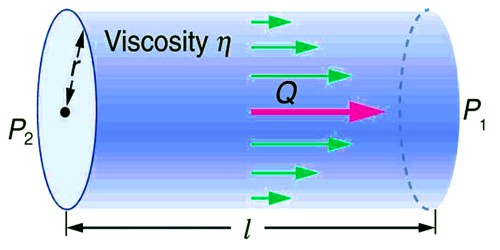
Poiseuille’s equation – Poiseuille investigated the balanced flow of a liquid through a capillary tube. He derived an expression for the volume of the liquid flowing per second through the tube.
V = πPr4 / 8 ηl
This is known as Poiseuille’s equation. Poiseuille developed an equation relating to the volume V of an out flowed water during the time t in a horizontal tube to the inside tube radius r (m), the fluid viscosity η, the length L of the tube and the fluid pressure p difference between the ends of capillary.
Practical applications
The importance of viscosity can be understood from the following examples.
(i) The knowledge of the coefficient of viscosity of organic liquids is used to decide their molecular weights.
(ii) The knowledge of the coefficient of viscosity and its variation with temperature helps us to choose a proper lubricant for definite machines. In heavy machinery, highly viscous oils (for example, grease) are used.