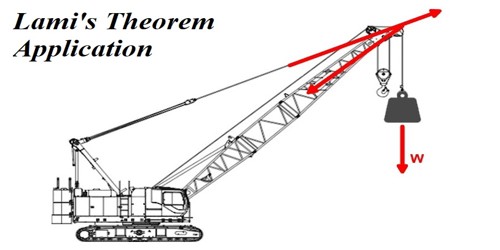
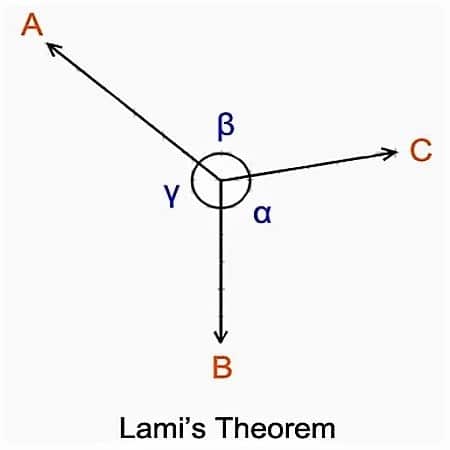
Lami’s theorem states that, if three concurrent forces act on a body keeping it in Equilibrium, then each force is proportional to the sine of the angle between the other two forces.
According to this theorem, when three coplanar, concurrent and non-co-linear forces act on a body which is in symmetry then the magnitude of each force is proportional to the sine of the angle between the other two forces.
Experimental Verification of Triangle Law and Lami’s Theorem:
Two smooth small pulleys are fixed, one each at the top corners of a drawing board kept vertically on a wall as shown in Figure. The pulleys should move freely without any friction. A light string is made to pass over both the pulleys. Two slotted weights P and Q (of the order of 50 g) are taken and are tied to the two free ends of the string. Another short string is tied to the center of the first string at O. A third slotted weight R is attached to the free end of the short string. The weights P, Q, and R are adjusted such that the system is at rest.
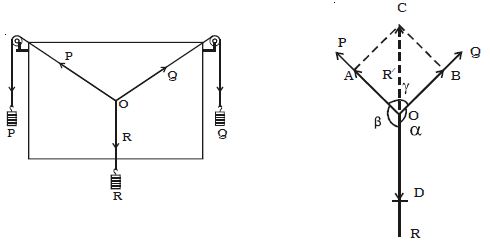
Fig: Lami’s theorem – experimental proof
The point O is in equilibrium under the action of the three forces P, Q and R acting along the strings. Now, a sheet of white paper is held just behind the string without touching them. The common knot O and the directions of OA. OB and OD are marked to represent in magnitude, the three forces P, Q, and R on any convenient scale (like 50 g = 1 cm).
The experiment is repeated for different values of P, Q, and R and the values are tabulated.
In statics, Lami’s theorem is an equation that relates the magnitudes of three coplanar, concurrent and non-collinear forces, that keeps a body in static equilibrium. Lami’s theorem states that if three forces acting at a point are in equilibrium, each force is proportional to the sine of the angle between the other two forces.
Consider three forces A, B, C acting on a particle or rigid body making angles α, β, and γ with each other.
Lami’s theorem is applied in static analysis of mechanical and structural systems. The theorem is named after Bernard Lamy.
If an object is in symmetry under the act of three forces, the consequential of two forces must be equivalent and contradictory to the third force. Thus, the line of action of the third force must pass from side to side the point of connection of the lines of action of the other two forces. In other words, the system of three coplanar forces in symmetry must obey the triangle law of forces and Lami’s theorem. This condition ensures the nonexistence of translational motion in the system.