Experiment: AC Circuit with Resistor

Let an alternating source of emf be connected across a resistor of resistance R.

The instantaneous value of the applied emf is

e = E₀ sin ωt … … (1)

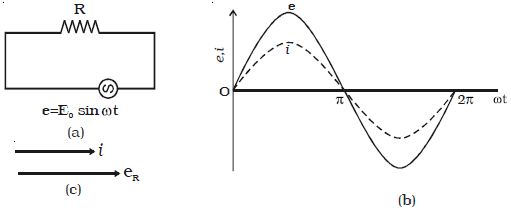
Fig: a.c. circuit with a resistor

If i is the current through the circuit at the instant t, the potential drop across R is, e = i R

Potential drop must be equal to the applied emf.

Hence, iR = E₀ sin ωt

i = E0/R sin ωt ; i = I₀ sin ωt …(2)

where I₀ = E0/R, is the peak value of a.c in the circuit. Equation (2) gives the instantaneous value of current in the circuit containing R.

From the expressions of voltage and current given by equations (1) and (2) it is evident that in a resistive circuit, the applied voltage and current are in phase with each other (Fig: b).

Figure: c is the phasor diagram representing the phase relationship between the current and the voltage.