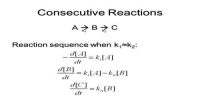Influence of Temperature on Reaction Rates
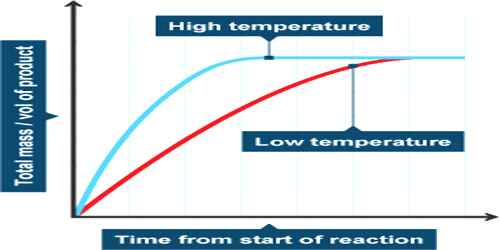
We know that, the rate of a reaction is affected by temperature. Increasing the temperature increases reaction rates because of the disproportionately large increase in the number of high energy collisions. It is only these collisions which result in a reaction.
The general effect of temperature on reaction rate is that in almost all cases an increase of temperature brings about an increase in the reaction rate. This shows up in the values of rate constants k (in rate laws) which is found to increase with the increase in temperature. The increase in the rate with increase in temperature is different for different reactions but an empirical fact is that the rate becomes approximately doable for each 10°C rise in temperature when the temperature is not much different from the room temperature. A quantitative expression for temperature dependence of reaction rate constants was proposed by S. Arrhenius in 1889. For most reactions the dependence could he expressed by the equation
k = A e –E/RT … … … (1)
In this equation, called the Arrhenius equation, e is the base of the natural logarithm scale, Ea is the activation energy, R is the gas constant and T is the temperature in degree Kelvin. A in the Arrhenius equation, which is assumed to be a constant for a particular reaction, is called the frequency factor. The frequency factor is related to the frequency of collision with proper orientation (in fact A has a slight dependence on temperature).
Taking the natural logarithm of both side of equation (1) one obtains,
ln k = ln a – Ea/RT … … … (2)
Convening from natural log to log to the base 10 equation (2) takes the form-
log k = logA = – Ea /2.303RT … … … (3)
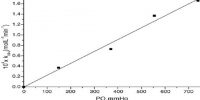
Equation (3) is in the form of an equation of a straight line, y = mx + c, in which one variable y is log k and the other x is 1/T. If log k is plotted against 1/T one obtains a straight line with the slope = — Ea/2.303R. The activation energy Ea can be calculated from the value of the slope. The intercept is log A from which the frequency factor A may be calculated.
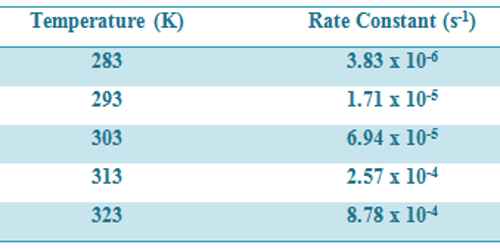
Some data for the decomposition of N2O5 at various temperatures are given in Table.
Table: Rate constants for decomposition of N2O5 at different temperatures-