Helmholtz free energy (work function) and its significance
In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature and volume. It is a measure of the functional work accessible from a stable temperature, constant volume thermodynamic system; more exactly, the dissimilarity between interior energy (of a system) and the product of its complete temperature and entropy.
This energy is stable at a stable temperature and volume. It plays a key role in statistical physics.
(a) Helmholtz free energy and maximum work
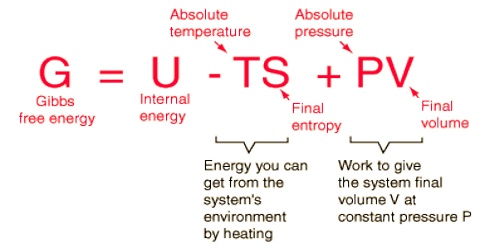
Like Gibbs free energy the Helmholtz free energy A is a state function. For the change in A,
∆A = ∆U – T∆S
If we consider an isothermal change at T, it can be shown, as in the case of Gibbs energy, by combining the first and second law of thermodynamics that,
– ∆A = Wmax
Where U is the internal energy, T is the fixed temperature and S is the entropy. The Helmholtz free energy is a determination of the energy required to create a system after the spontaneous energy transfer from the environment has taken place. The quantity TS is the energy you can get from the system’s environment by heating. The above definition may be obtained from the internal energy function by means of one Legendre transform.
Thus the decrease in this Free Energy is equal to the maximum work done by the system in an isothermal process at constant volume. The Helmholtz free energy function is called a ‘work function’, because of the relationship between A and w. The part of internal energy which is used in useful work called Helmholtz’s free energy (A). It stays constant during any isothermal-isochoric change. For such a system, this free energy tends to minimize as the system tends to equilibrium.
Actually ‘Helmholtz free energy’ is created only for convenience. It is used in the calculation of thermodynamic properties from assessable quantities like temperature, pressure, volume, etc.
(b) Helmholtz free energy, spontaneity and equilibrium
For constant volume processes the relations of ∆A to spontaneity and equilibrium may be summarized as follows:
∆A < 0 (negative); the process is spontaneous
∆A > 0 (positive); the process is non-spontaneous
∆A = 0; the system is at equilibrium.
Application of Helmholtz free energy
- In the equation of state: Pure fluids with high precision (like industrial refrigerants) are represented using Helmholtz function as a sum of an ideal gas and residual terms.
- In auto-encoder: It is a simulated neural network which is used to instruct competent data. Here Helmholtz energy is used to find the sum of code cost and reconstructed code.