Work of Expansion
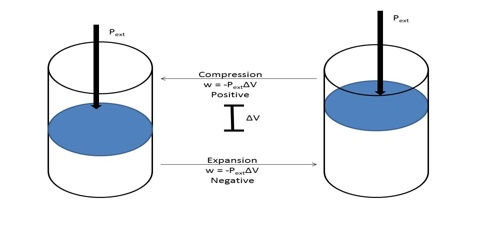
The work involved in the change of volume of a gas against an external pressure is of considerable interest to chemists. The work done as a result of expansion of the gas is the work of expansion. In thermodynamics, however, work has a very specific meaning: it is the energy it takes to move an object against a force. Work, w, is one of the fundamental ways energy enters or leaves a system, and it has units of Joules. Consider a gas contained in a cylinder (Figure) of cross-sectional area, a. fitted with a weightless and friction-less piston.
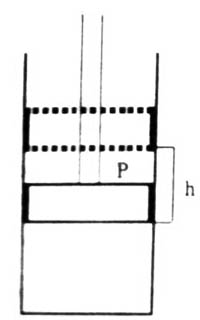
Fig: Expansion of Gas
When the pressure on the piston is P it comes to an equilibrium position. The force on the piston is P x a. i.e., the pressure multiplied by the area. Let the gas in the cylinder expand, when-the piston is raised by a distance, h. As the point of application of the force has been displaced by h the work done against the force is P x a x h. But a x h is equal to the change in volume, ∆V. Hence the work of expansion will be;
w = – P x ∆V … … … (1)
The negative sign in equation (1) indicates that the work is done by the gas on the surrounding. In equation (1), ∆V (= Vf–Vi) is the change in volume, where Vf and Vi are the final and initial volume of the gas respectively. For expansion of gas ∆V > 0 and P x ∆V is a negative quantity.
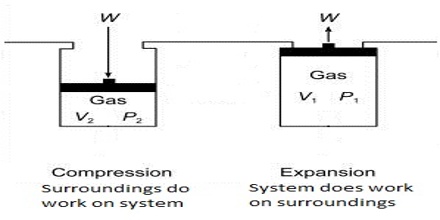
For compression (work, done on the system) ∆V< 0, and P x ∆V is a positive quality. If the gas is an ideal one, P∆V may be replaced by RT for one mole and work of expansion equals RT. The units in which work is expressed will depend on the units of P and V.