Instantaneous acceleration: If the time interval approaches zero, the rate of change of velocity with time of a body is called the instantaneous acceleration or simply acceleration.
Explanation: Let the change of velocity at exceedingly small time interval ∆t be ∆v→. Then instantaneous acceleration is obtained by dividing ∆v→ by the exceedingly small time during which change of velocity has taken place. The limit of a rate as the denominator approaches zero is called a derivative. Instantaneous acceleration is then the limit of average acceleration as the time interval approaches zero — or alternatively, acceleration is the derivative of velocity.
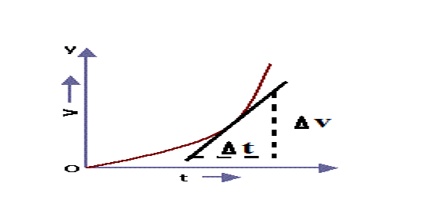
So, instantaneous acceleration, a = lim∆t→0 ∆v→/∆t = dv→/dt
Hence, instantaneous accelerations may be defined as follows: If the time interval tends to zero, the limiting value of average acceleration is equal to the acceleration
The magnitude of acceleration is, a = │dv→/dt│
It is to be mentioned that instantaneous acceleration at any point is along the perpendicular direction of the velocity of the body at that point.
Acceleration is again divided into two types: Variable acceleration and Uniform acceleration.