The reflectance and transmittance are defined in terms of the rate of energy flow incident on unit area of the interface, Si • (- ei) = Si cos θi. Thus the reflectance and transmittance are
R = (Sr cos θr)/ (Si cos θi); T = (St cos θt)/ (Si cos θi)
Where,
S = ε E2 vp ≈ (n2 ε0) E2 (c/n)
is the magnitude of the Poynting vector, and the cos θ factors take account of the projected area of the interface as seen by the incoming and outgoing waves. Hence
R = |r|2; T = (nt/ni) (cos θt / cos θi) t2 = 1 – R
For the case of internal reflection we see that as θi → θc both amplitude reflection coefficients obey r → 1, while the amplitude transmission coefficients remain finite. However, because cos θt → 0 as θi → θc, while cos θi → cos θc which is finite, from Equation we must have T → 0 as θi → θc. It is straightforward to show that R + T = 1, as required by energy conservation. The reflectance is shown in below Figure for the cases of (a) external reflection and (b) internal reflection.
Notice that for the case of external reflection shown in Fig (a) and grazing incidence, i.e.. θi → 90°, the reflectance approaches 100% (R → 1). This phenomenon is used in the design of imaging X-ray space telescopes, and a typical design based on XMM-Newton is sketched in below Figure.
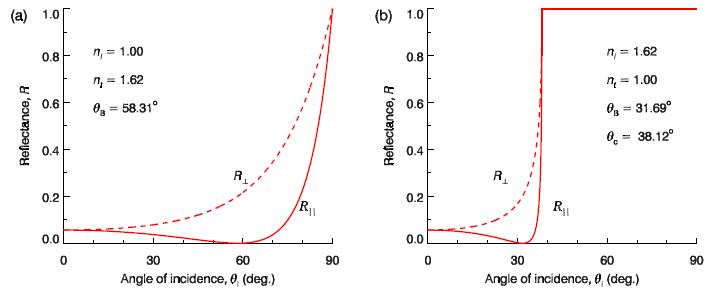
Figure: Reflectance for (a) external reflection off flint glass and (b) internal reflection within flint glass.