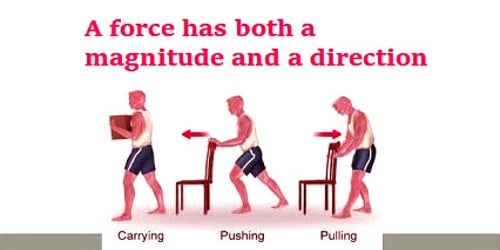
The magnitude of the force is defined as the sum of all the forces acting on an object. Calculating magnitudes for forces is a vital measurement of physics. The ‘magnitude’ of a force is its ‘size’ or ‘strength’, in spite of the path in which it acts. When you’re functioning in one dimension, the magnitude of the force isn’t impressive you have to think about. For example, the force of a 2-pound weight in your hand, pushing down, has the similar magnitude as a 5-pound pull on a rope, a 5-pound push on a wall, or a 5 pound-force pushing up against the ceiling. The equation below is the sum of N forces acting on an object.
The magnitude of the force is F = BIl sin θ
(i) If the conductor is placed along the direction of the magnetic field, θ = 0o, Therefore force F = 0.
(ii) If the conductor is placed perpendicular to the magnetic field,
θ = 90o, F = BIl. Therefore the conductor experiences a maximum force.
Calculating magnitude is more of a dispute in two or more dimensions because the force will have “components” along both the x- and y-axes and perhaps the z-axis if it’s a three-dimensional force. Theoretically, these forces are uneven, because they all have dissimilar directions. But their magnitudes are all the similar.
First of all, force is a vector quantity. It has direction and magnitude. Now the magnitude of the force can be calculated by finding out the amount of acceleration it offers to a body,
Using F= ma. Where,
M → mass and, a → aceeleration provided mass are constant.