The electric machine in which mechanical energy is converted into electrical energy is called generator. The basic principals of this machine are established on the basis of electromagnetic induction. Generator can be of two kinds. Such as
1) AC generator
2) DC generator
AC generator: The structure and functions of it are being discussed in the following as it is widely used:
Structure: There is a field-magnet NS in it. There is rectangular coil of wire in the middle of the magnet on the soft sheet of iron (AB). The iron sheet is called armature. The armature is rotated at the uniform speed in mechanical way on the middle of the magnet. The two sides of the rectangular coil are connected to two slip rings.
The two slip rings can rotate to same orbit of armature. The two carbon brushes are set in such a way that they touch the two slip rings when the armature is being rotated. The resistance R of external circuit is connected to the brushes.
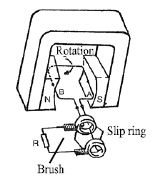
Functions: When the armature undergoes rotation, the armature coil intersect the lines of force of the magnetic field and the electromotive force is induced in the coil according to electromagnetic induction. As the two sides of the coil are connected to the external circuit a alternating current is develop in the circuit. The magnitude of induced current mainly depends on the intensity and speed of the rotation of the magnetic field. During one complete rotation of the coil the direction of the induced curent is changed once. Thus the alternating current is produced from the mechanical energy.









