Integration
Suppose a quantity is dependent on another quantity, then in mathematical language this dependent quantity becomes function of the other quantity. If quantity y is dependent on x, then y is function of x.
Let the length of a rod be x, and the rod is divided into innumerable equal segments. Length of one of these segments = dx. If we add all these small segments we can find the length x of the entire rod.
∑dx = x … … … (1)
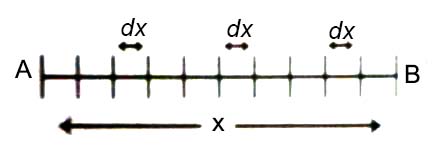
Here symbol ∑ expresses integration.
Equation (1) can be written in the following way,
∫dx = x … … … (2)
“∫” symbol also indicates integration. It is seen from this equation that integral value of dx is equal to x. So, we can say that integration is a term of summation. In order to bring equality in both sides of the above equation a constant of integration c is added and written as:
∫dx = x + c.
Again, let integral value of a function, ∫f(t) dt = A(x).
Then f(t) is called the integral quantity. dt after f(t) indicates that the integration is to be done with respect to t. It is called variable.