Angular displacement is defined,
Δθ = (arc length / radius) = s/r
For a full circle θ = 2π rad. Note that rad is not a unit, but rather a placeholder. Thus, “rad” may appear and disappear from equations. The angular velocity is defined:
ω = Δθ/Δt → (ω) = rad/s
and angular acceleration,
α = Δω/Δt → (α) = rad/s2
If T is the period, i.e., the time for one revolution is the average speed and is given by,
ωave = 2π red / T
Solution
We have the period for the second hand Tsecond = 60 s, so that
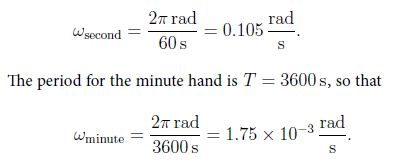
Discussion: Another unit for angular speed in common use is revolutions per minute (rpm). Then ωsecond = 1 rpm and ωminuite = 60-1 rpm = 0.0167 rpm.
The Rotational kinematics equations are derived the same way as in the case of linear equations. For α = const, we find the average velocity ωave = (ω0 + ω)/2 = (ω0 + αt/2), so that for the angular displacement we have ΔΔ = ωave t = ω0 + at2/2. We eliminate the time from the equation for the angular velocity t = (ω – ω0) / α, so that ΔΔ = ωave t = (w0+w)/2 * (w0+w)/α, We thus arrive at the kinematics equation for rotation,
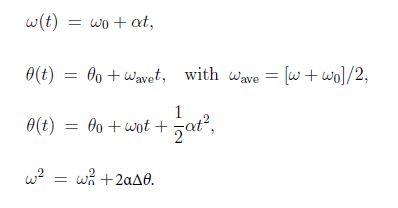
We note that these equations are identical to Equations, when quantities for linear motion (x, v, a) are replaced by the respective quantities for rotational motion (θ, ω, α).