Angle of Minimum Deviation (δm)
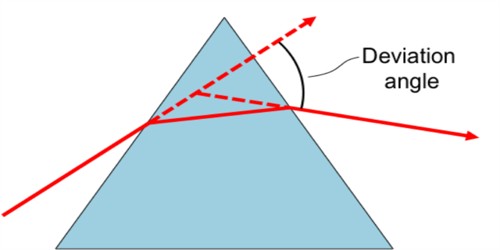
We know, when a ray of light passes through a prism deviation takes place due to refraction of light and the angle between the incident and emerging rays represents the angle of deviation. The value of this angle of deviation depends on the angle of incidence. Starting from a small value of the angle of incidence if it is gradually increased then the angle of deviation also continues to and for a particular value of the angle of incidence, the angle of deviation becomes minimum [Figure).
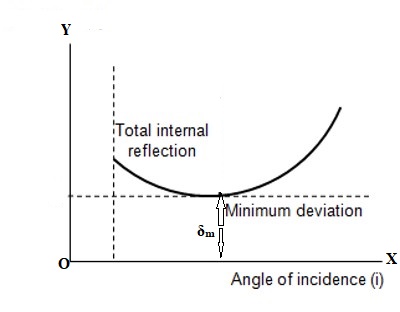Afterward, if the angle of incidence is increased, the angle of deviation also increases. This minimum value of the angle of deviation is called the angle of minimum deviation. It is denoted by δ3 or Dm.
Definition: The angle of deviation becomes, minimum for a particular angle of incidence of the incident ray on a prism. This minimum value of the angle of deviation is called the angle of minimum deviation.
The angle of deviation through a triangular prism is defined as the angle between the incident ray and the emerging ray (angle δ). It can be shown that when the angle of incidence i is equal to the angle of refraction r’ for the emerging ray, the angle of deviation is at a minimum.
The position of the prism for which the angle of minimum deviation is round, that position is called the position of minimum deviation.
If a curve is drawn by plotting the angle of incidence i1 along X-axis and angle of deviation δ along Y-axis, then the value of the angle of deviation becomes minimum for a particular angle of incidence. This is the angle of minimum deviation. In the figure, δm is the angle of minimum deviation.
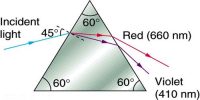
From the experimental results it is found that in case of an angle of minimum deviation, i1 = i2 and r1 = r2. So, a ray of light obeys the following conditions in case of an angle of minimum deviation.
Conditions for minimum deviation
There are three conditions for the minimum deviation, viz –
(1) In case of minimum deviation, ∠i1 = ∠i2 = (∠A + δm) / 2
(2) In case of minimum deviation, ∠r1 = ∠r2 = ∠A/2
(3) A ray of light travels symmetrically through the prism in case of minimum deviation. That means, from the edge of the prism the distances of the point of incidence of the ray of light on the first and the second refracting surfaces will be equal [in fig, AQ = AR]. In this condition, the refracted ray will be parallel to the base of the prism.
