Derivation of Equation for Kinetic Energy
In case of translational motion: Amount of work done by a moving body before coming to rest is the measure of kinetic energy.
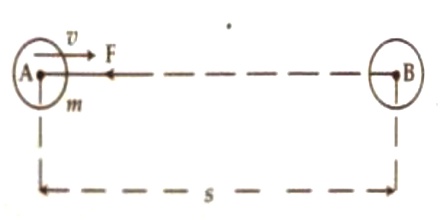
Suppose, a body of mass ‘m’ is moving along AB with a velocity v. A constant force F is applied opposite to the motion along BA. Due to this uniform retardation will be produced. Let the uniform retardation = a and the body came to rest at point B after covering a distance s from point A. Here, final velocity. v = 0.
Kinetic energy = work done before coming to rest
= force x distance travelled before coming to rest = F x s
We know from Newton’s second law of motion;
Force = mass x acceleration or retardation
means, F = ma
According to description, 0 = v2 – 2as
or, 2as = v2; or, s = v2/2a
Putting the values of F and s in the above equation, we get,
Kinetic energy = ma x v2/2a = ½ mv2
or, K. E. = ½ mv2
That means, kinetic energy (K.E.) = ½ mv2 = ½ mass x (velocity)2