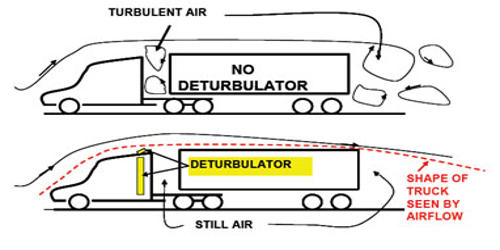
Stokes’s law finds application in a number of areas, generally with regards to the settling of sediment in clean water and in measurements in the viscosity of parachute.
Stoke performed many experiments on the motion of small spherical bodies in different fluids and concluded that the viscous force F acting on a spherical body of radius r depends directly on –
- radius (r) of the sphere
- velocity (v) of the sphere and
- coefficient of viscosity η of the liquid
Therefore F ∝ η x r yvz ⇒ F = kηxr y vz, where k is a dimensionless constant.
Using dimensions, the above equation can be written as
[MLT-2] = k [ML-1T-1]x × [L]y × [LT-1]z
On solving, we get x = 1, y = 1, and z = 1 Therefore, F=kη rv
Experimentally, Stoke found that the value of k = 6π
F = 6πη rv.
This relation is known as Stoke’s law. The law, first set forth by the British scientist Sir George G. Stokes in 1851, is derived by consideration of the forces acting on a particular particle as it sinks through a liquid column under the influence of gravity.
Application
Falling of raindrops: When the water drops are small in size, their terminal velocities are small. Raindrop do not acquire alarmingly high velocity during their free fall. If this does not happen a person moving in the rain would get hurt. Since the raindrops are smaller in size and their terminal velocities are small, remain suspended in the air in the form of clouds. Therefore they remain suspended in the air in the form of clouds. As they grow up in size, their terminal velocities increase and they start falling in the form of rain.
But as the drops combine and grow in size, their terminal velocities increase because, v ∞ a2. Hence they start falling like rain. This law explains the following:
- Floatation of clouds.
- Larger raindrops hurt us more than the smaller ones.
Come down from parachute: While jumping from an airplane, parachute helps us to land safely on the earth. A man coming down with the help of a parachute acquires constant terminal velocity. Stoke’s law helps a person coming down by making use of a parachute, to reduce.
Stoke’s law explains why the speed of a raindrop is below a freely dropping body with continuous velocity, from the height of clouds.
Stokes’ law, with a modified form of Ladenburg’s wall-correction factor, has been applied to determine the viscosity of glass from the velocity of a freely falling platinum sphere. The reproducibility of results is excellent and good agreement has been obtained using spheres of different diameters, indicating the use of the revised wall-correction factor.