When several resistances are connected in such a way that one terminal of all the resistances is joined at a common point A and the other terminals are joined at another common point B and the potential difference across each of the resistors remains the same, then this combination of resistances is called parallel combination of resistances.
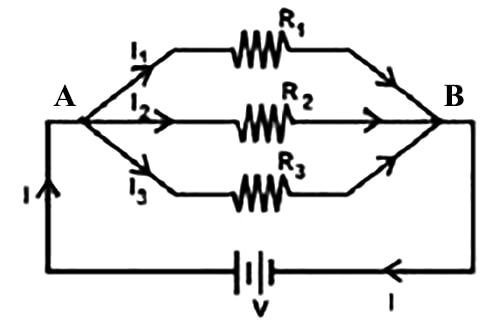
Fig: Parallel Combination of Resistances
Three resistors R1, R2 and R are connected in a parallel combination. In this case, the same potential difference V is maintained across the two terminals of the three resistors. Different amount of current is flowing through each of the resistors owing to their different values. The main current I of the circuit splits into three parts at the junction a and later recombine at the point b. Let I1, I2 and I3 are the currents flowing through the resistances R1, R2 and R3 respectively. Therefore, some of the currents I1, I2 and I3 of parallel paths is equal to the current I at the junction a.
Therefore, I = I1 + I2 + I3
Here, the potential difference between the two terminals being V, applying Ohm’s law we get,
I1 = V/R1 , I2 = V/R2, I3 = V/R3
If instead of three resistances, n numbers of resistances are connected in parallel then the equivalent resistance Rp can be expressed as;
1/RP = 1/R1 + 1/R2 + 1/R3
That is, resistances connected in a parallel combination, the sum of the inverse of the individual resistances is equal to the inverse of the equivalent resistance.