A typical n-alkane (n-nonane) is shown in the figure
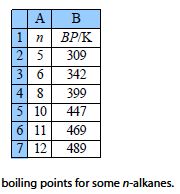
The boiling points (BP/K) of some liquid n-alkanes of formula CnH2n+2 are believed to fit the formula shown below. This is an example of the type of equation that organic Chemists use to model large amounts of tabulated data. Clearly here we are using a very small data sample but increasing the number of data points will increase the precision and usefulness of the equation and the model equation will then be a convenient summary.
BP = A log (n+B) – C
Type up your own spreadsheet and solve it for the arbitrary constants (A, B, and C) to find the model equation from the data below the figure, and then interpolate to find the boiling point of n-nonane and the precision of the predicted boiling point.
Solution: Boiling point of n-Alkanes
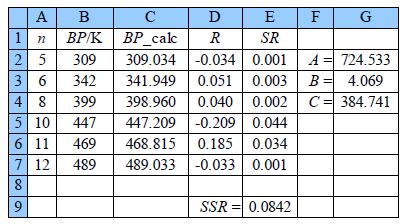
The above Figure shows the spreadsheet for using Solver, column C has the calculated boiling point using the model equation with C2 having the equation,
= $G$2* LOG(A2 + $G$3) — $G$4
typed in the formula window. Cell D2 has =B2 — C2, and E2 has = D2^2 entered. The rest of columns C, D, and E are filled in by copying and pasting. The SSR is in cell E9 with =SUM(E2:E7) entered.
We need to find reasonable initial starting values for the arbitrary constants. If you type in unity (1) in G2, G3, and G4 then the SSR is over a million and is dearly wrong. The boiling points are in the range of 300-400 K which arises very approximately as the difference between A and C. So typing in a few values by hand then A = 700 and C = 300 gives SSR = 8234, which is a lot smaller than a million. The constant B fine tunes the boiling point for changes in the chain length of the alkane. So stating from B = 1 try some numbers and you find that B = 2 gives an SSR = 765. This should be a good enough starting point for the DEPS algorithm to find the global minimum.
Placing the cursor on cell E9 click on Tools, Solver. The target cell should be $E$9, click on minimize, and select cells G2 to G4 to change. In the Options of the Solver, the window makes sure the algorithm used is DEPS, edits learning cycles from 2,000 to 2,000,000 and the stagnation limit from 70 to 70,000. Click on OK and then Solve. Stagnation is reached after 9.59 seconds on my laptop with the final results shown in above Figure with SSR = 0.0842.
Now we have the global minimum for the model equation of the boiling points we need to manually vary each constant in turn and look for the changes in SSR by a factor of 10. Such an approach quickly gives us estimates of the precisions of the arbitrary constants, A is precise to ±0.1; B to ±0.01; and C to ±0.1. The NLLSQ fit of the model equation for the six n-alkanes is shown below in Figure shows the data and our fitted NLLSQ equation.
BP = (724.5± 0.1K )log (n + (4.07± 0.01))— (384.7± 0.1K )
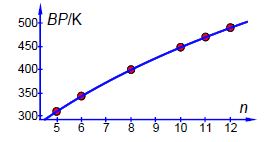
The boiling point of n-nonane is interpolated from our NLLSQ equation as,
BP = (724.5± 0.1 K)log + (4.07± 0.01))- (384.7± 0.1K )
BP = (424.0 ↑ 424.5 ↑ 423.6)K
BP= 424.0±0.5K
Our NLLSQ equation may be used to interpolate the missing boiling points for ri = 7 and n = 9 with a confidence of ±0.5 K. However, extrapolating outside the range of n values for other alkanes is much less certain and should be treated with extreme caution.