Constant Pressure Processes and Enthalpy
In chemistry constant pressure processes are more common than constant volume processes since most reactions are usually carried out in open vessels under atmospheric pressure. Under a certain constraint pressure, gases can expand or contract; depending on the type of constraint, the final state of the gas may change.
A convenient thermodynamic function enthalpy, or heat content is used to describe a constant pressure process. This function is represented by the letter H and is defined by;
H = U + PV … … … (1)
Like any other thermodynamic state function it is impossible to determine the absolute value of enthalpy of a system. The enthalpy of a system depends only on the state of the system and is in no way affected by the way in which the state is reached. When a system changes from state 1 to state 2 the value of ∆H, (i.e., H2 – H1), is constant, no matter how the system undergoes change in going from the initial state to the final state. In thermodynamic treatments we are concerned with ∆H. As will be seen, for solids and liquids ∆H values are usually almost equal to the change in internal energy, ∆U. This is because solids and liquids are only slightly compressible; i.e., their volume changes only to a small extent when the pressure is changed. Under constant pressure conditions equation may be written as,
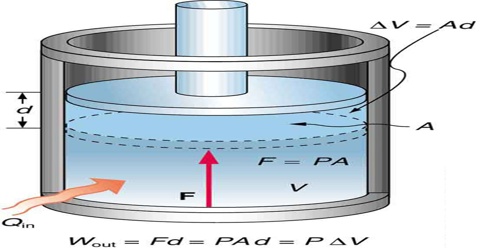
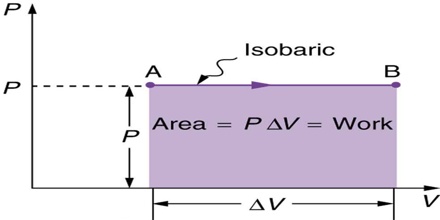
dU = qP – P.dV
qP = dU + P.dV (as w = P.∆V)
= U2 – U1 + P (V2 – V1)
= (U2 + PV2) – (U1 +PV1) … … … (2)
qP, being the heat absorbed at constant pressure.
As H = U + PV, equation (2) takes the form,
qP = H2 – H1 = ∆H
In other words, the heat absorbed under constant pressure conditions is equal to the increase in enthalpy or heat content, if the only work done is the pressure volume work.
Example: What will be the change in enthalpy when 5.0 mol of iron is heated from 90°C to 140°C at atmospheric pressure?
(specific heat of Fe is 0.4476 J g-1 deg-1)
Ans: We know, ∆H = qP = (sp.heat) m ∆T
∆H = (5.0 x 55.8) (0. 0.4476) (140 – 90) = 6.25 kJ