Describe on Equilibrium Constant Kp

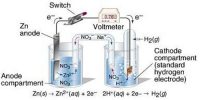
If we express a gas-phase equilibria in terms of partial pressures, we obtain the equilibrium constant Kp. For the reaction below:

CO (g) + 3H₂ (g) = CH₄ (g) + H₂O (g)

The equilibrium-constant expression in terms of partial pressures becomes:

K_P = (P_CH4 P_H2O)/(P_CO P_H2)

In general, the numerical value of Kp is not the same as the value of Kc. From the relationship P V = n R T, we show that

Kp = Kc (RT)^Δn

Where: An is the total amount of moles of gaseous product LESS the total amount of moles of gaseous reactant. Consider the following reaction:

2SO₂ (g) + O₂ (g) ↔ 2SO₃ (g)

Reaction constant Kc for the reaction is 2.8 x 10² at 1,000 °C. Calculate Kp for the reaction at this temperature.

We know that: Kp = Kc (RT)^Δn

From the equation we see that Δn = 2 – (2 +1) = -1. We can simply substitute the given reaction temperature and the value of R (0.08206 dm³.atm/molK) to obtain Kp.

Thus,

Kp = 2.8 x 10² x (0.08206 x 1,000)^-1

Kp = 3.4