Determination of charge of an electron – Millikan’s oil drop experiment
Millikan’s experiment is used for the measurement of the charge of an electron.
Principle
This method is based on the study of the motion of uncharged oil drop under free fall due to gravity and charged oil drop in a uniform electric field. By adjusting the uniform electric field suitably, a charged oil drop can be made to move up or down or even kept balanced in the field of view for a sufficiently long time and a series of observations can be made.
Experimental arrangement
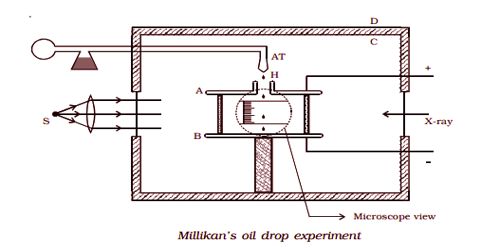
The apparatus consists of two horizontal circular metal plates A and B, about 22 cm in diameter and separated by a distance of about 16 mm as shown in Fig 6.5. The upper plate has a hole (H) in the middle. These plates are held together by insulating rods of glass or ebonite so that they are perfectly parallel to each other.
The plates are surrounded by a constant temperature bath D and the chamber C containing dry air. The plates are connected to a battery which can provide a potential difference of the order of 10000 V.
Theory
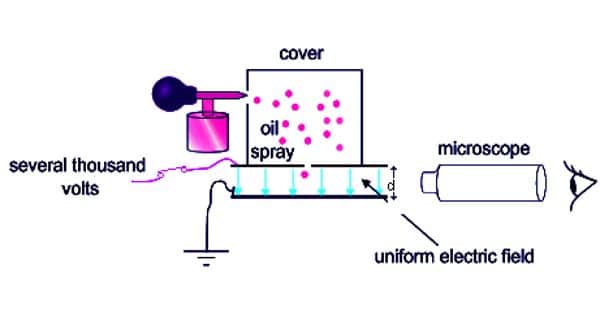
A spray of fine droplets of a highly viscous liquid (such as glycerine) is produced by means of an atomizer (AT) near the hole H and enter the space between A and B. The droplets are illuminated by an arc lamp L and are seen through a microscope whose eyepiece is provided with a micrometer scale. One such droplet is viewed through the microscope as it descends under gravity. The viscous force due to air increases and soon it attains a constant terminal velocity and let it be v. The terminal velocity v of the droplet is measured using the microscope.
(i) Motion under gravity
The gravitational force acting on the oil drop downwards is equal to mg = 4/3 πa3 ρg, where a is the radius of the oil drop, ρ is the density of the oil, and g, the acceleration due to gravity.
The upthrust experienced by the oil drop due to the displaced air is 4/3 πa3 σg, where σ is the density of air.
So, The net downward force acting on the oil drop = weight of the oil drop – upthrust experienced by the oil drop.
= 4/3 πa3 ρg – 4/3 πa3 σg
= 4/3 πa3 (ρ – σ) g … … … … (1)
Since the oil drop attains a terminal velocity v, the net downward force acting on the oil drop is equal to the viscous force acting opposite to the direction of motion of the oil drop.
By Stoke’s law, the viscous force on the oil drop is 6πaηv, where η is the co-efficient of the viscosity of air.
4/3 πa3 (ρ – σ) g 6πaηv …. …. … … (2)
The radius of the oil drop is,
a = [9ηv / 2(ρ – σ)g]1/2 …. … …(3)
(ii) Motion under the electric field
The air inside the parallel plates is ionized by sending a beam of X-rays. The droplets pick up one or more electrons from the ionized air.
Let q be the charge carried by the droplet under observation. Let E be the electric field applied between the plates A and B, so that the drop moves upwards with a terminal velocity v1, which can be determined using the microscope.
The force on the droplet due to the electric field is Eq. Since the velocity of the droplet is uniform, we have
Eq = 4/3 πa3 (ρ – σ) g + 6πaηv1
Eq – 4/3 πa3 (ρ – σ) g = 6πaηv1 … … … (4)
Adding equations (2) and (4),
Eq = 6πaη (v + v1) …. ….. ….. (5)
Substituting the value of ‘a’ in equation (5) from equation (3),
Eq = 6πη3/2(v + v1) [9v/2(ρ – σ)g]1/2…. … …(6)
If V is the potential difference between A and B, d is the distance between them, then E = V/d
Millikan determined the value q for a large number of oil drops using equation (6) and found that they are an integral multiple of the least value. The greatest common factor gives the charge e of the electron.
The charge of an electron was found to be: 1.602 × 10-19 coulomb.