Energy of Simple Harmonic Motion
Simple harmonic motion is any periodic, repetitive motion where a restoring force is applied that is proportional to the displacement, in the opposite direction of that displacement. For example, when you pull a spring, the force trying to yank the spring back to its original position increases and increases. If you pull that spring out and let go, it will bounce back and forth around a middle, equilibrium position. This motion back and forth is simple harmonic motion.
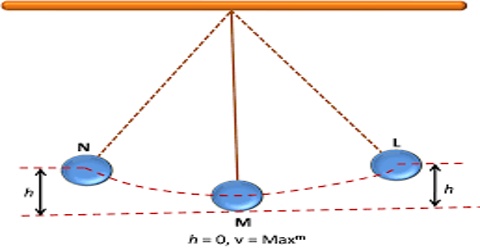
Motion of a simple pendulum is simple harmonic motion. When pendulum oscillates its kinetic energy is some position converted into potential energy and in other positions potential energy is converted into kinetic energy. But the sum total of potential and kinetic energy remains constant.
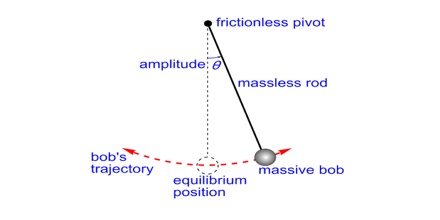
Suppose, the mass of the bob of a simple pendulum is in and its equilibrium position is at 0. Let the bob reach the maximum point B in one direction by travelling a distance A [Figure]. At point B, since velocity v = 0, its total energy is potential energy. If the force acting on the simple pendulum is F, than F = – kx. So at point B, maximum potential energy,
EP = A∫0 – F dx = A∫0 – kx dx
= k [x2/2]A0 = ½ kA2