Frequency of Collisions of Gas Molecules
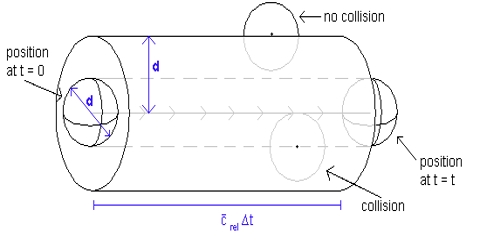
The number of collisions undergone by a molecule of gas in one second, i.e., the frequency of collisions, may be calculated from the mean free path and the average velocity. If a molecule travels, on an average, a distance l cm before being hit by another molecule and its average velocity is C; then the number of collisions that this particular molecule will undergo in one second in a volume of 1/mL is given by:
C/l = [√(8RT/πM) / {1/(√2πσ2n)}]
= 4 σ2n √(πRT/M)
Since there are n molecules in unit volume, the total number of collisions undergone by all the molecules in 1 mL is the product of the right hand side of equation above and n. But in this calculation each collision has been counted twice – once when the molecule hits another molecule and again when it is hit by another molecule. The correct number of collisions is obtained by introducing a factor ½ in the product, so that the frequency of collisions, Z, is given by-
Z = (½ n) 4σ2n√(πRT/M)
= 2 4σ2n2 √(πRT/M)
Example:
Calculate the frequency of collisions for oxygen molecules at 0°C and 1 atm pressure. Collision diameter = 3.64 x 10-8 cm.
Solution;
n = (6.02×1023/22,414) = 2.58×1019
Z = 2 (3.64 x 10-8)2 x (2.58×1019)2 x [√{(3.14)(8.32×107) x (273.16)}/32]
= 9.02 x 1028 mL-1s-1
It may be seen from the example that the frequency of collisions between molecules is rather high, about 1028 collations in 1mL in one second even at ordinary temperature. When the temperature increases the frequency of collisions also increases.