Deduction of the Gas Laws from the Kinetic Equation
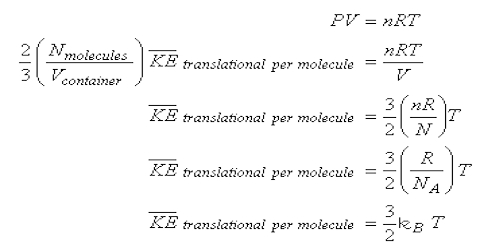
All the gas laws may be deduced from equation: PV = 1/3 mnc2 … … (1)
This is the kinetic equation for gases. Although the above deduction has been made for a cubical vessel the equation is valid for a vessel of any shape as the vessel can be divided into a large number of small cubes for each of which this equation is valid.
(a) Boyle’s law: Boyle’s law states the relationship between volume and pressure at constant temperature and mass. Temperature is a measure of the kinetic energy of the molecules. The higher the temperature higher is the kinetic energy of the molecules Equation (1) may be written in the form.
PV = (2/3 x 1/2) mnc2 = 2/3 x total Kinetic Energy … … (2)
Since the kinetic energy of a moving body is – ½ mc2. For a given quantity of gas, when the temperature is constant, the kinetic energy is constant. Hence,
PV = constant (at constant T) which is Boyle’s law. In other words according to Boyle’s law volume is inversely proportional to pressure when the temperature and the number of molecules are constant.
Charles’ or Gay-Lussac’s law: The total kinetic energy of the molecules is proportional to the absolute temperature. i.e K.E. = const x T (hence from equation 2)
PV = const x T
In his experiment, he calculated that the increase in volume with every degree equals 1/273.15 times of the original volume. At constant volume for a given quantity of gas P ∞ T., This is Charles’ or Charles’ or Gay-Lussac’s law. According to his findings, at constant pressure and for constant mass, the volume of a gas is directly proportional to the temperature. This means that with the increase in temperature the volume shall increase while with decreasing temperature the volume decreases.
Avogadro’s law: According to Avogadro’s law, at constant temperature and pressure, the volume of all gases constitutes an equal number of molecules. Consider that two gases are at the same pressure, P, and contained in vessels of equal volume, V. Both the vessels are at the same temperature. For the first gas, from the kinetic equation (1)
PV= 1/3 n1m1c12
Where n1 is the number of molecules, m1, is the mass of each molecule and c1 is the r.m.s. velocity. Similarly, for the second gas;
PV = 1/3 n2m2c22
Where n2, m2, and c2 have the same significance as for the first gas. Since P, V and T of the two gases are the same, according to equation (1)
1/3 n1m1c12 = 1/3 n2m2c22 … … … (3)
At the same temperature, the Kinetic Energy of the molecules of both the gases are the same; that is,
1/2 m1c12 = 1/2 m2c22 … … … (4)
If equation (3) is divided by equation (4) One obtains; n1 = n2
That is, the number of molecules in equal volumes of the two gases under the same conditions of T and P is the same. This means that at an unchanged temperature and pressure conditions, the molar mass of every gas is directly proportional to its density. This implies that in unchanged conditions of temperature and pressure the volume of any gas is directly proportional to the number of molecules of that gas. This is Avogadro’s hypothesis or Avogadro’s law.