Equation of State of a Gas Mixture: Dalton’s Law of Partial Pressure
When two or more gases are placed in the same container it is experimentally observed that the pressure of the gas mixture is related to the volume of the container and the temperature by the same expression as in the case of a single gas, i.e.,
PV = nRT …. ….. ….. (1)
Here n stands for the total number of moles of gases in the container.
The behavior of a mixture of gases is summarized in Dalton’s law of partial pressures (1801). Dalton’s law of partial pressure states that,
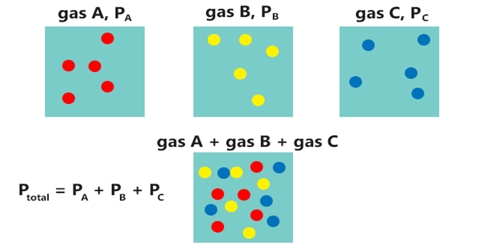
“The total pressure exerted by a mixture of gases is the sum of the partial pressures of the individual gases”
The partial pressure of a component gas in a stature is defined as;
“The pressure that the gas would exert if it were present alone in the container at the same temperature; i.e , if it occupied the same volume”
The total pressure P for a mixture of gases would, therefore, be equal to the sum of the partial pressures p1, p2, p3 etc. of these gases.
P = p1, + p2 + p3 + … …
If the volume in which the gas mixture is places is V, then according to the definition of partial pressure;
p1 = n1 (RT/V); p2 = n2 (RT/V); p3 = n3 (RT/V)
Hence, P = (n1 + n2 + n3 + …).(RT/V) = n(RT/V)
This result shows that the expression PV = nRT can be used for a mixture of gases as well as for pure gases.
It must be realized that the Dilton’s law has the same limitations as the equation of state for gases.
Example: 4.00 L of Nitrogen at a pressure of 4.0 atm pressure and 1.00 L of Oxygen at a pressure of 2.0 atm are introduced into 3 container of volume 2.0 L. Calculate the total pressure of the gas mixture in the container.
Solution: The partial pressure p2 of nitrogen in the container can be obtained from the relation-
p1V1 = p2V2
p2 = p1V1/V2
= [(4.00×4.0)/2.0] = 8.0 atm
Similarly the partial pressure p3 of Oxygen in the container; (2.00×2.0)/2.0= 1.0 atm.
Adding p2 and p3 we obtain the total pressure = 8.0 + 1.0 = 9.0 atm.