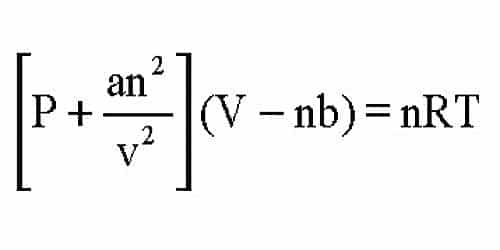Significance and Limitations of van der Waals Equation
The success of the van der Waals equation lies in the fact that it can explain the variation of PV with P in Amagat’s curves. At very low pressures both “a and b” may be neglected as the molecules are far apart and b is an insignificant fraction of V. The constant ‘a’ provides an alteration for the intermolecular forces. Constant ‘b’ is a rectification for finite molecular size and its value is the volume of one mole of the atoms or molecules. The equation takes the form PV = RT. When the pressure is slightly greater, b may be neglected compared to V and the van der Waals’ equation may be written as:
(P + a/V2)V = RT
or, PV = RT – (a/V)
PV is less than RT by a/V, PV is decreased with increases of P.
The van der Waals’ equation may also write as;
P(V-b) + a/V2(V-b) = RT
or, P(V-b) + a (1/V – b/V2) = RT
At high pressures (1/V – b/V2) becomes negligible as the two terms are not very much different from one another. Neglecting the second term on left-hand side one obtains.
P (V – b) = RT
or PV = RT x Pb
According to the equation, PV increases with an increase of P. These deductions are in agreement with Amagat’s observation that for real gases with the increase of P the value of PV first decreases passes through a minimum and then gradually increases. It may be observed that at low pressures the pressure correction has prominence, while when the pressure is high the volume correction predominates.
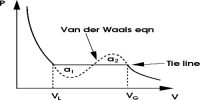
In the case of hydrogen and helium the values of “a” arc smaller than those of “b” so that the volume correction predominates all along with the range of pressures. PV increases as P is increased at ordinary temperatures. A point is considerable importance is that the van der Waals’ equation is also applicable to gas-liquid transitions and liquids. The agreement of PV values calculated from van der Waals equation with experimental result for ethylene at 20°C. It is evident that over a wide range of pressures PV varies considerably but the values are in agreement with those calculated from van der Waals’ equation.
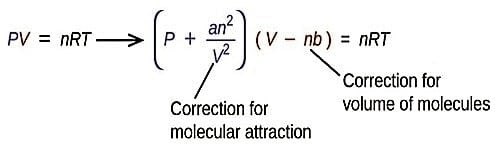
Limitations of van der Waals Equation –
The success of van der Waals equation should not, however, overshadow its limitations. At very high pressure the equation is inadequate for calculating the properties of gases. Moreover, the experiment shows that the values of ‘a’ and ‘b’, which were regarded as constants by van der Waals, change when the temperature is varied. Also, ‘b’ is not constant at all pressures.
The values of constant ‘a’ and ‘b’ obtained by different methods differ considerably. Although Van Der Waals theory assumes them to be constant. The value of ‘a’ is found to depend on the temperature. At very high temperatures, it tends to zero.
(i) The value of ‘b’ is not constant but varies with pressure and temperature. As the temperature reaches extremes, real gas starts to deviate from Van der Waals equation.
(ii) The value of VC is not equal to 3b, but actually, it is equal to, in some case; and in other cases 2b.
Thus no gas obeys Van Der Waals equation closely in the vicinity of the decisive point. As the temperature reaches extremes, real gas starts to deviate from Van der Waals equation.
Example: Calculate the pressure exerted by one mole of carbon dioxide in a 500 mL container at 300 K using van der Waals’ equation. For CO2 the values of the constants are: a = 3.61 L2 atm-mol-1, b = 0.0429 L mol-1, and R = 0.082 L-atm mol-1K-1. Compare this value with the value obtained by using the ideal gas equation.
Solution: V = 500 mL = 0.50 L;
Substitution in equation gives;
(P + 3.61/0.502) (0.50-0.0429) = 0.082×300
On calculation it is findout P = 39.4 atm.
Ideal gas equation gives P = RT/V = (0.082×300)/0.50 = 49.2 atm