Heat, Internal Energy, and Work: Relation
We know, when a gas expands, it itself does some work on the surroundings. On the other hand when a gas contract, work is done on the system by the surroundings. Now we will find an expression for work done by the system during expansion. Heat flows from the body at a higher temperature to the one at a lower temperature. The flow stops when the temperatures es will be equal and the two bodies are then in thermal equilibrium. Heat is energy that flows between a system and its environment by virtue of a temperature difference between them.
Let C be a cylinder made of the conductor of heat. Let a certain amount of gas be filled in the cylinder and closed by light, frictionless, and airtight piston. As a result, the piston can move without a resistance. It is to be noted that the piston is also a bad conductor [Figure]. If the pressure of the enclosed gas is P and area of cross-section of the cylinder is A. then the force applied by the gas on the piston,
F = pressure x area of cross-section of the piston
= P x A
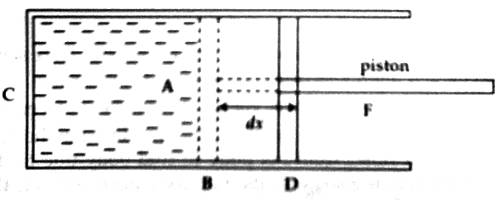
Let us consider that the gas is expanded at constant pressure. As a result, the piston has moved from position B to position D and traveled a distance dx. So, work done
dW = Force x Acceleration
or, dW = F x dx = PAdx
or, dW = P.dV
Here A.dx = dV = increase in the volume due to expansion of gas.
That is, Work = Pressure x Change of volume
This work is called external work.
[Work done in expansion of a gas is positive and work done in compression is negative]
If the initial volume of the gas is V1 and the final volume after expansion is V2, then work done by the gas,
dW = P(V2 – V1)
If during expansion, pressure also changes, then,
dW = dP.dV = (P1 – P2) (V2 – V1)
Here, P1 = initial pressure of the gas, P2 = a final pressure of the gas. If P is expressed in Nm-2 and volume in m3, then the unit of work will be Joule (J).
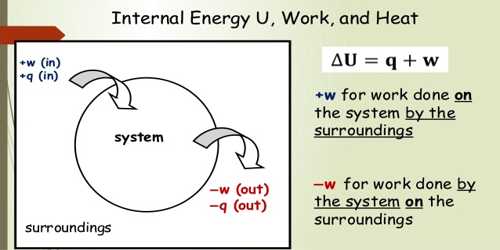
From the first law of thermodynamics we know if the change of internal energy of a system is du and external work done is dW due to the supply of heat dQ in the system, then
dQ = du + dW
or, dQ = du + PdV
or, dQ = du + P (V2 – V1)
Equations (1) and (2) are the relations between heat, internal energy, and work in isobaric process.