The capacitance of a Spherical Conductor
Capacitance is the ability to store electrical energy. Almost all things, including you, can store some electrical energy and therefore have capacitance. When you rub your feet across a carpet, charged particles called electrons can be transferred from the carpet to you. The capacitance of a spherical conductor is directly proportional to its radius.
Spherical Capacitor is the capacitance for spherical or cylindrical conductors that can be obtained by evaluating the voltage difference between the conductors for a given charge on each. It is a kind of capacitor that has one or more thin hollow spherical plate/s conductors. Spherical capacitors can be of various types namely Isolated Spherical Capacitor, Concentric Spherical Capacitors with two spheres, etc. It depends then on the inner and outer radius of each sphere.
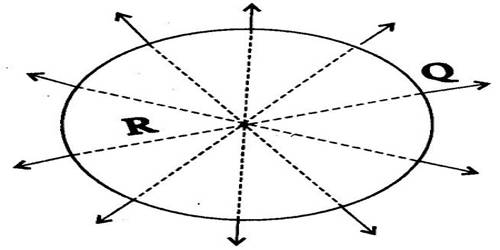
Suppose the center of a spherical conductor A of radius r (m) placed in a vacuum or in the air is O and contains +Q amount of charge [Figure]. Let the capacitance of the sphere be C and its surface potential be V. Now, according to the definition of capacitance,
C = Q/V or, V = Q/C … …. …. (1)
We know charges distribute uniformly all over the surface of a conductor. So, it will appear that all the lines of force are coming out from the center of the sphere. Even if we consider the ‘Q’ amount of charge at the center O of the sphere, lines of force will come out similarly. Thus in case of a charged spherical conductor, it may be considered that all the charges are concentrated at the center.
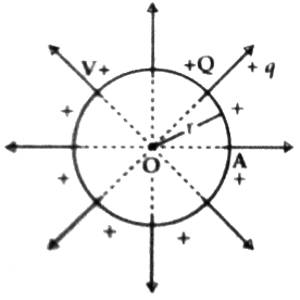
Potential on the surface of the spherical conductor,
V = 1 / 4πε0 x Q/r … … … (2)
From equations (1) and (2) we get,
Q/C = 1 / 4πε0 x Q/r
so, C = 4πε0 r … …. (3)
(1) For a medium of dielectric constant εr, potential on the sphere, V = Q / 4πε0 r
so, C = Q/V = 4πε0εr r … … … (4)
Here, ε0 = 8.854 x 10-12 Coulomb2 / Newton-meter2 (C2/N-m2).
(2) “1 Farad capacitance of a conductor” means that in order to increase its potential by 1 volt 1 coulomb of charge is needed to give and the capacitance of the conductor is equal to the capacitance of a spherical conductor in the vacuum or in the air having a radius of 9 x 109 m.
(3) From equation (3), the unit of ε0 Farad/meter (F/m).
Working exercise: Of the two metallic spheres of the same radius one is hollow and the other one is solid. If they are changed at the same potential in which one more charges will remain?
The capacitance for spherical conductors can be obtained by evaluating the voltage difference between the conductors for a given charge on each. The capacitance of any sphere (C = 4πε0R), whether hollow or solid, will be the same if the surrounding medium is the same. Again, if the surrounding medium is air, then capacitance C = 4πε0R, where R = radius of the sphere. The above two spheres have an equal radius. So, their capacitances will be the same. If the applied potential is V, then a charge of each of the spheres will be Q = CV. So, in the two spheres, an equal amount of charge will remain.