Dimension: We have discussed earlier that according to the origin quantities are of two types-one is fundamental quantity and the other is compound quantity. Also we know that those quantifies which do not depend on other quantities are called fundamental quantities.
Definition of dimension of any quantity may be given by any one of the following:
(1) The symbol which is used to express a relation between a quantity and its fundamental unit is called dimension of that quantity. For example, length is a quantity. Foot or centimetre or metre is its fundamental unit. Symbol is used to express the relation between length and its fundamental unit. Here means length. Again, each of the terms such as foot or centimetre or metre also expresses the length. So symbol ‘L’ is the symbol signifying the relation between length and its fundamental unit.
(2) Dimension of any physical quantity establishes the relation between that quantity and its fundamental unit.
(3) In order to form a derived unit power through which the fundamental unit is raised, that power is called the dimension of the derived unit.
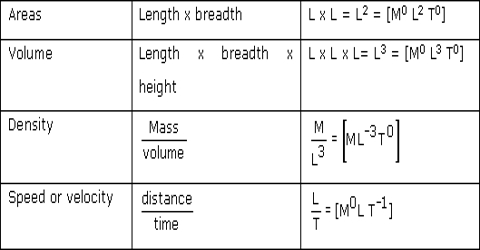
Dimensional equation: The three fundamental units in physics are length, mass and time. Their dimensions are respectively L M and T. As length is expressed by L, so length is one L-dimensional quantity. Area is length x length= L x L= L2. So, area is two L-dimensional quantity. Similarly, volume is length x length x length = L x L x L = L3. So, volume is three L-dimensional quantity. Hence, [L].[L2].[L3] are called dimensional equation. Dimensional equation may be defined in the following way:
The fundamental equation which expresses relation between fundamental unit and derived unit is called Dimensional equation.